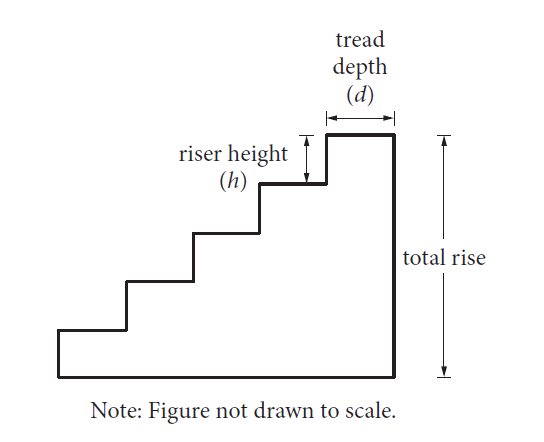
When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
Some building codes require that, for indoor stairways, the tread depth must be at least 9 inches and the riser height must be at least 5 inches. According to the riser-tread formula, which of the following inequalities represents the set of all possible values for the riser height that meets this code requirement?
0≤h≤5
h≥5
5≤h≤8
8≤h≤16
The correct Answer is:C
Since the tread depth, d, must be at least 9 inches, and the riser height, h, must be at least 5 inches, it follows that d ≥ 9 and h ≥ 5, respectively. Solving for d in the risertread formula 2h + d = 25 gives d = 25 − 2h. Thus the first inequality, d ≥ 9, is equivalent to 25 − 2h ≥ 9. This inequality can be solved for h as follows:
−2h≥9−25
2h≤25−9
2h≤16
h≤8
Therefore, the inequality 5 ≤ h ≤ 8, derived from combining the inequalities h ≥ 5 and h ≤ 8, represents the set of all possible values for the riser height that meets the code requirement.
Choice A is incorrect because the riser height, h, cannot be less than 5 inches. Choices B and D are incorrect because the riser height, h, cannot be greater than 8. For example, if h = 10, then according to the riser-tread formula 2h + d = 25, it follows that d = 5 inches. However, d must be at least 9 inches according to the building codes, so h cannot be 10.
Similar Questions
The inequation represented by the graph given below is :
02:10View SolutionThe inequation that best describes the graph given below is _________
02:17View SolutionThe inequation that best describes the following graph is _________
02:10View SolutionWhich inequations represent the shaded region in the given figure
04:23View Solution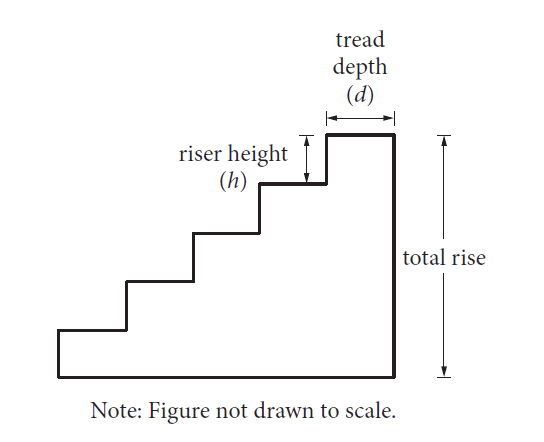
When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
Which of the following expresses the riser height in terms of the tread depth?View Solution
When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
An architect wants to use the riser-tread formula to design a stairway with a total rise of 9 feet, a riser height between 7 and 8 inches, and an odd number of steps. With the architect’s constraints, which of the following must be the tread depth, in inches, of the stairway? (1 foot = 12 inches)View SolutionA stairway of 20 ft height is such that each step account for half a foot upward and one foot forward. What distance will an ant travel if it strats from ground level to reach the top of the stairway ?
02:49View Solution

