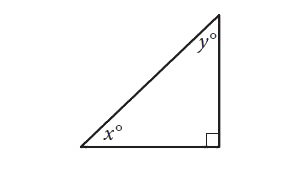
In the triangle above, the sine of x∘ is 0.6. What is the cosine of y∘ ?
Video Solution
Text Solution
The correct Answer is:6 or35
The angles marked x∘ and y∘are acute angles in a right triangle. Thus, they are complementary angles. By the complementary angle relationship between sine and cosine, it follows that sin(x∘)=cos(y∘). Therefore, the cosine of y∘ is .6. Either .6 or the equivalent fraction 35 may be gridded as the correct answer.
Alternatively, since the sine of x∘ is .6, the ratio of the side opposite the x∘ angle to the hypotenuse is .6. The side opposite the x∘ angle is the side adjacent to the y∘ angle. Thus, the ratio of the side adjacent to the y∘ angle to the hypotenuse, which is equal to the cosine of y∘, is equal to .6.
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
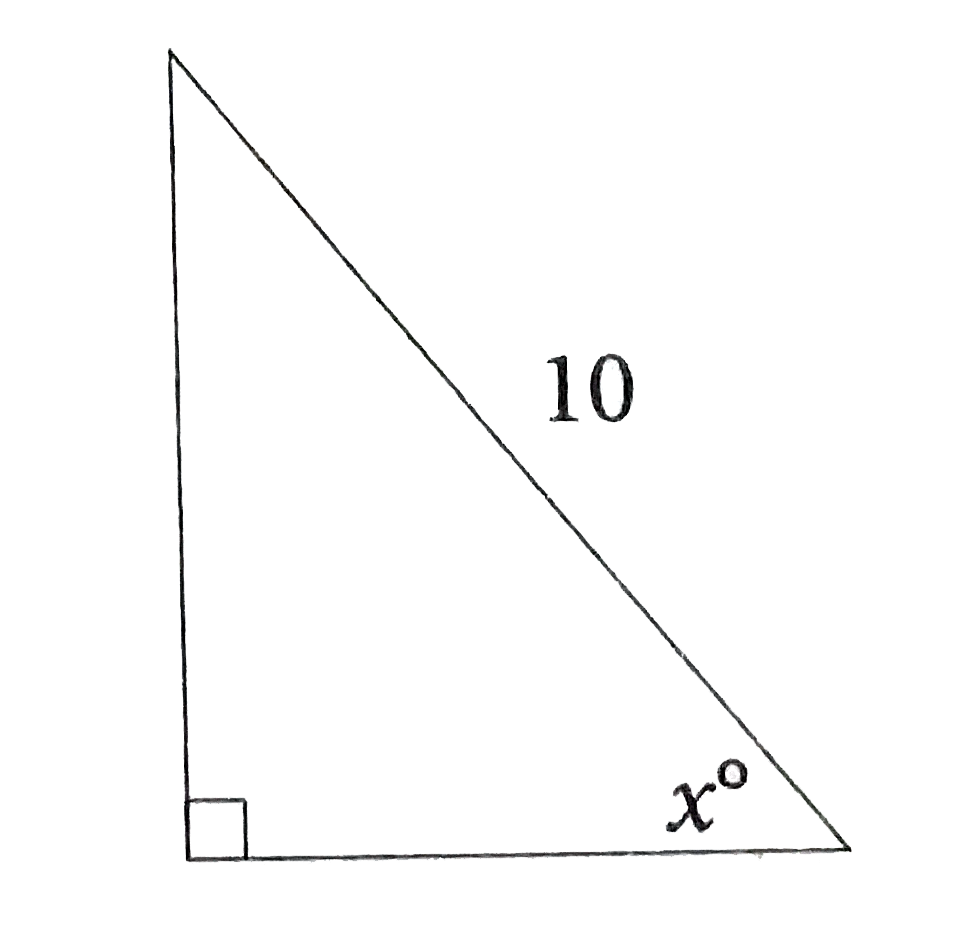
In the triangle above, sin x=0.8 and cos x=0.6. What is the area of the triangle?A0.48B4.8C24D48 - Question 2 - Select One
What is the sine of ∠A in the triangle below?
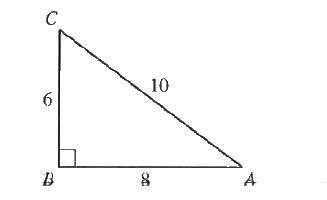 A0.30B0.50C0.60D0.75
A0.30B0.50C0.60D0.75
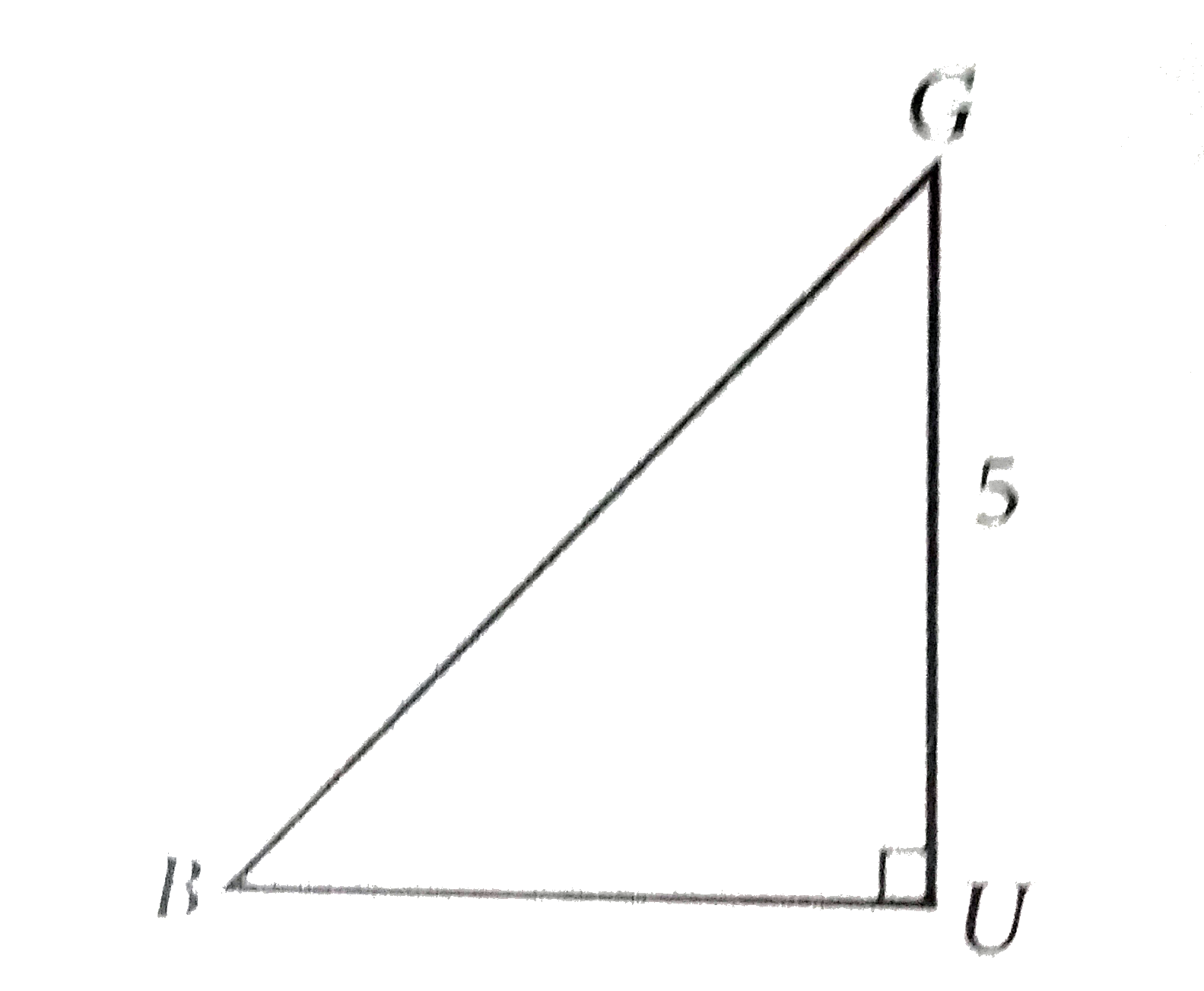
Triangle BUG shown is an isosceles right triangle. If the length of side UG is 5 units, what is the sine of ∠G?View SolutionIf the area of the triangle formed by the pair of lines 8x2−6xy+y2=0 and the line 2x+3y=a is 7 then a=
View Solution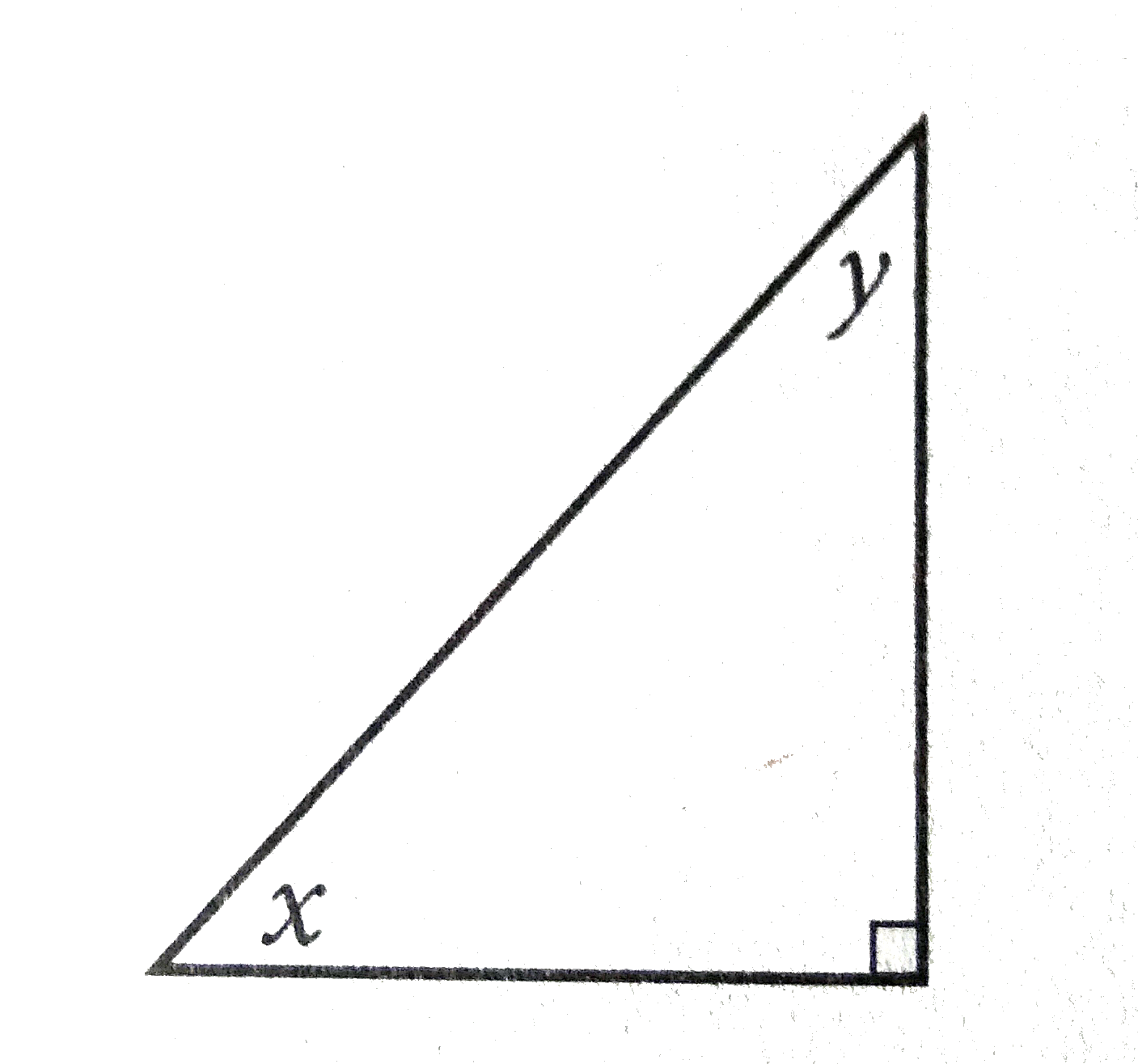
The right triangle above, cosx=0.8. What is the value of cosy?View Solution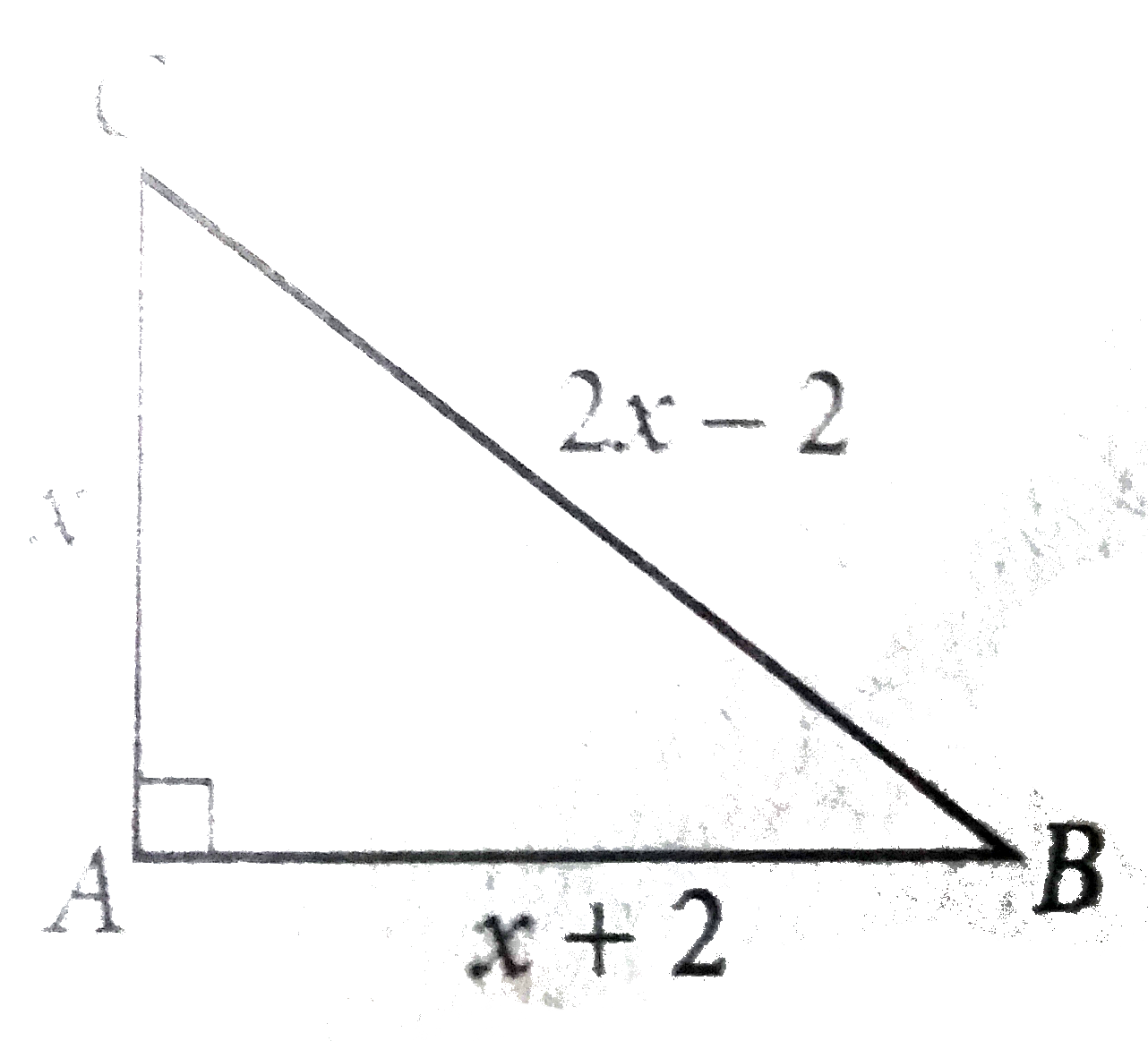
In the figure above, △ABC is a right triangle. What is the value of x?View SolutionStatement -1 : The circumcentre of the triangle formed by the lines x + y = 0 , x - y = 0 and x + 5 = 0 ( - 5 , 0) .
Statement-2 : Cicumcentre of a triangle lies inside the triangleView SolutionThe orthocentre of the triangle formed by the lines x−7y+6=0,2x−5y−6=0and7x+y−8=0 is
View Solution

