Mr. Martinson is building a concrete patio in his backyard and deciding where to buy the materials and rent the tools needed for the project. The table below shows the materials’ cost and daily rental costs for three different stores.

The total cost, y, for buying the materials and renting the tools in terms of the number of days, x, is given by y=M+(W+K)x .
If the relationship between the total cost, y, of buying the materials and renting the tools at Store C and the number of days, x, for which the tools are rented is graphed in the xy-plane, what does the slope of the line represent?
The total cost of the project
The total cost of the materials
The total daily cost of the project
The total daily rental costs of the tools
The correct Answer is:D
The total cost, y, of buying the materials and renting the tools in terms of the number of days, x, is given as y = M + (W + K)x. If this relationship is graphed in the xy-plane, the slope of the graph is equal to W + K, which is the daily rental cost of the wheelbarrow plus the daily rental cost of the concrete mixer, that is, the total daily rental costs of the tools.
Choice A is incorrect because the total cost of the project is y. Choice B is incorrect because the total cost of the materials is M, which is the y-intercept of the graph of y = M + (W + K)x. Choice C is incorrect because the total daily cost of the project is the total cost of the project divided by the total number of days the project took and, since materials cost more than 0 dollars, this is not the same as the total daily rental costs.
Similar Questions
The area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View SolutionIf y-x=180^(@) then find the values of x and y. ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_034_Q01.png" width="80%"gt
View SolutionMr. Martinson is building a concrete patio in his backyard and deciding where to buy the materials and rent the tools needed for the project. The table below shows the materials’ cost and daily rental costs for three different stores.
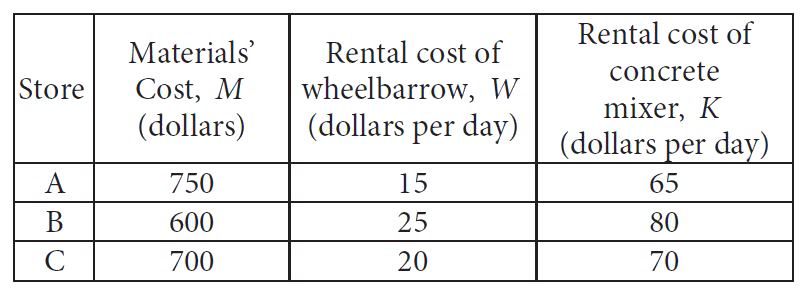
The total cost, y, for buying the materials and renting the tools in terms of the number of days, x, is given by y=M+(W+K)x .
For what number of days, x, will the total cost of buying the materials and renting the tools from Store B be less than or equal to the total cost of buying the materials and renting the tools from Store A ?
View Solution
