h(x)=1(x−5)2+4(x−5)+4
For what value of x is the function h above undefined?
To determine the value of x for which the function h(x) is undefined, we need to analyze the denominator of the function. The function is given as:
h(x)=1(x−5)2+4(x−5)+4
Step 1: Set the denominator equal to zero
For the function h(x) to be undefined, the denominator must be equal to zero. Therefore, we set up the equation:
(x−5)2+4(x−5)+4=0
Step 2: Substitute y=x−5
To simplify the equation, we can let y=x−5. Substituting this into the equation gives us:
y2+4y+4=0
Step 3: Factor the quadratic equation
Next, we can factor the quadratic equation. The expression y2+4y+4 can be recognized as a perfect square:
(y+2)2=0
Step 4: Solve for y
Setting the factored form equal to zero gives us:
(y+2)2=0
This implies:
y+2=0
Thus, solving for y:
y=−2
Step 5: Substitute back to find x
Now, we substitute back for y:
x−5=−2
Solving for x:
x=−2+5=3
Conclusion
The function h(x) is undefined at:
3
---
For the function h(x) to be undefined, the denominator must be equal to zero. Therefore, we set up the equation:
To simplify the equation, we can let y=x−5. Substituting this into the equation gives us:
Next, we can factor the quadratic equation. The expression y2+4y+4 can be recognized as a perfect square:
Setting the factored form equal to zero gives us:
Now, we substitute back for y:
The function h(x) is undefined at:
Similar Questions
Knowledge Check
For which values of x in the expression 3x+63x(4x+8)(x−5) undefined?
A−2B−2,5C0,−2,5D0,2,−5y=3h−2x+5
hy−8x=5
For what value of h does the system of equations above have no solution?A165B138C1115D58If (2)/(5)(5x)+2(x−1)=4(x+1)−2, what is the value of x?
Ax=−2Bx=2CThere is no value of x for which the equation is trueDThere are infinitely many values of x for which the equation is true
For what value of x, the matrix [5−xx+124] is singular?
View Solution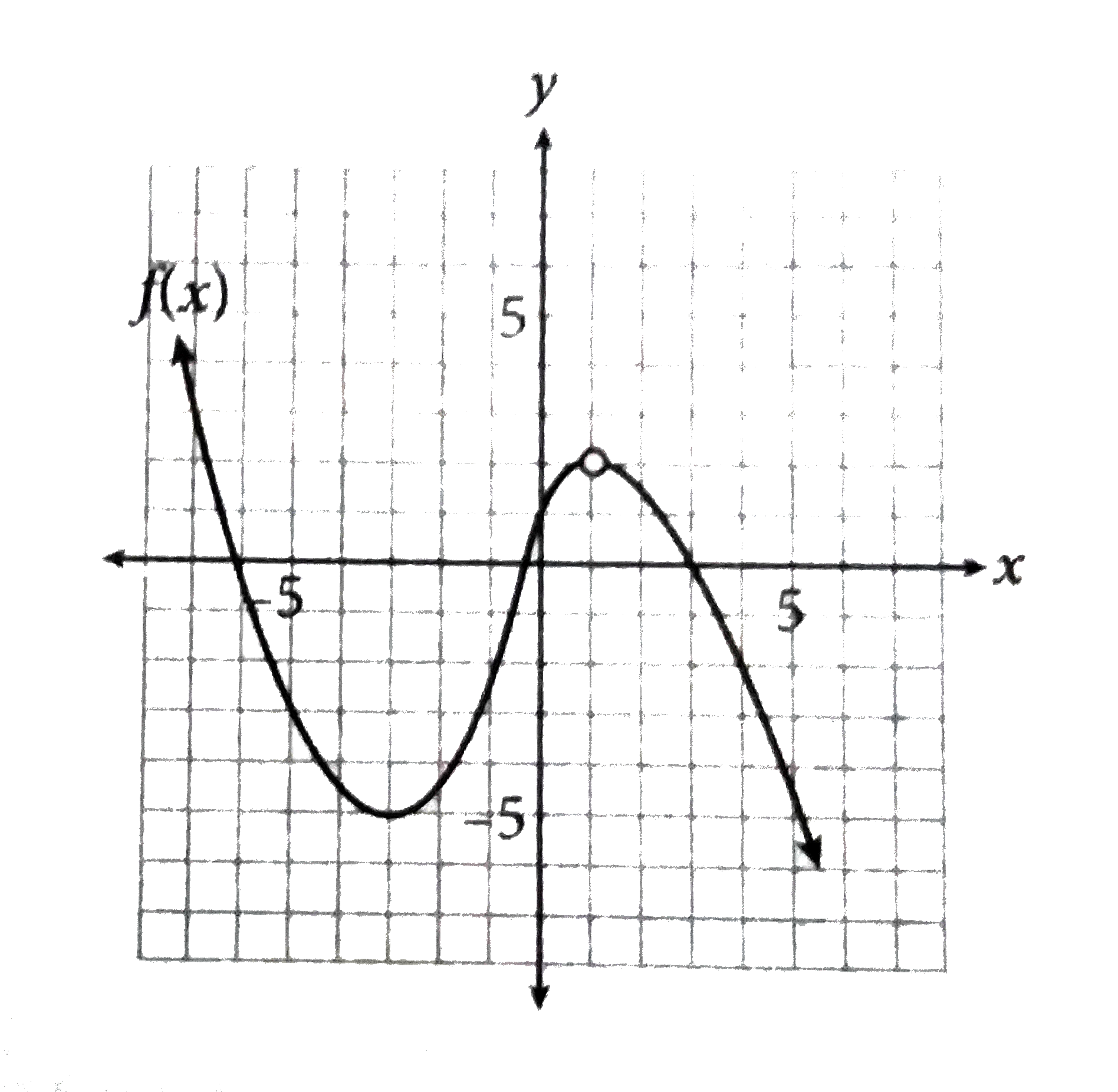
The graph of y=f(x) is given above. For what value of x is y=f(x-4) undefined?
View SolutionIf h=x2−1x+1+x2−1x−1, what is x in terms of h?
View SolutionWhat values for x would make 1√x+1 undefined ?
View Solutionx2−4x−5(x−1)2−4(x−1)
The expression above is equivalent to
View Solution
