y=3
y=ax2+b
In the system of equations above, a and b are constants. For which of the following values of a and b does the system of equations have exactly two real solutions?
a = −2, b = 2
a = −2, b = 4
a = 2, b = 4
a = 4, b = 3
To solve the problem, we need to determine the values of a and b such that the system of equations:
1. y=3
2. y=ax2+b
has exactly two real solutions.
1. Set the Equations Equal to Each Other:
We start by equating the two equations:
ax2+b=3
Rearranging gives us:
ax2+b−3=0
2. Identify the Quadratic Form:
This is a quadratic equation in the standard form px2+qx+r=0, where:
- p=a
- q=0 (since there is no x term)
- r=b−3
3. Determine the Discriminant:
The discriminant d of a quadratic equation is given by:
d=q2−4pr
Substituting our values:
d=02−4(a)(b−3)=−4a(b−3)
4. Condition for Exactly Two Real Solutions:
For the quadratic equation to have exactly two real solutions, the discriminant must be greater than zero:
−4a(b−3)>0
5. Analyze the Inequality:
To solve the inequality −4a(b−3)>0, we can divide both sides by -4 (remembering to reverse the inequality):
a(b−3)<0
This means that a and (b−3) must have opposite signs.
6. Check Possible Values of a and b:
We need to test the given options for a and b to see which pair satisfies the inequality a(b−3)<0.
- Option A: a=−2,b=2
−2(2−3)=−2(−1)=2(not less than 0)
- Option B: a=−2,b=4
−2(4−3)=−2(1)=−2(less than 0)
- Option C: a=2,b=2
2(2−3)=2(−1)=−2(less than 0)
- Option D: a=2,b=4
2(4−3)=2(1)=2(not less than 0)
From the checks, we find that Option B (a=−2,b=4) satisfies the condition for exactly two real solutions.
Final Answer:
The values of a and b for which the system of equations has exactly two real solutions are:
(−2,4)
2. y=ax2+b
We start by equating the two equations:
ax2+b=3
Rearranging gives us:
ax2+b−3=0
This is a quadratic equation in the standard form px2+qx+r=0, where:
- p=a
- q=0 (since there is no x term)
- r=b−3
The discriminant d of a quadratic equation is given by:
d=q2−4pr
Substituting our values:
d=02−4(a)(b−3)=−4a(b−3)
For the quadratic equation to have exactly two real solutions, the discriminant must be greater than zero:
−4a(b−3)>0
To solve the inequality −4a(b−3)>0, we can divide both sides by -4 (remembering to reverse the inequality):
a(b−3)<0
This means that a and (b−3) must have opposite signs.
We need to test the given options for a and b to see which pair satisfies the inequality a(b−3)<0.
−2(2−3)=−2(−1)=2(not less than 0)
- Option B: a=−2,b=4
−2(4−3)=−2(1)=−2(less than 0)
- Option C: a=2,b=2
2(2−3)=2(−1)=−2(less than 0)
- Option D: a=2,b=4
2(4−3)=2(1)=2(not less than 0)
The values of a and b for which the system of equations has exactly two real solutions are:
(−2,4)
Similar Questions
Knowledge Check
−3x + y = 6
ax + 2y = 4
In the system of equations above, a is a constant. For which of the following values of a does the system have no solution?A−6B−3C3D63x−7y=12,kx+21y=−35
For which of the following values of k will the system of equations above have no solution?A9B3C−3D−9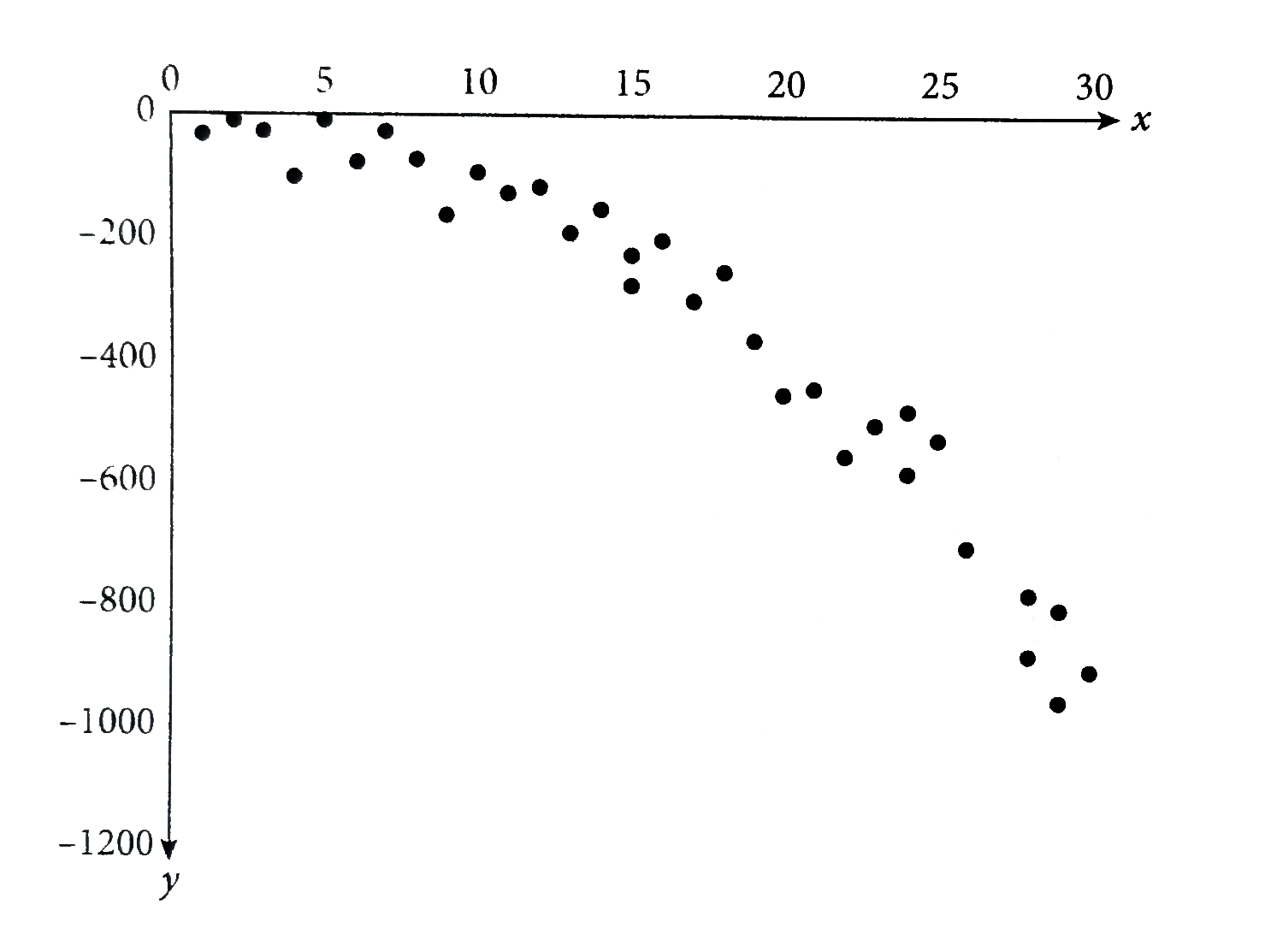
For which of the following values of a and b does the equation y=axb model the data in the scatterplot above ?Aa<0,b<0Ba<0,b>0Ca>0,b<0Da>0,b>0
kx−3y=4
4x−5y=7
In the system of equations above, k is a constant and x and y are variables. For what value of k will the system of equations have no solution?
View Solution4x+6y=12
y=80−kx
For what value of k does the system of equation above have no solution?
View SolutionIf the system of linear equations above has o solution, and a is a constant, then what is the value of a ?
View Solutiony=3h−2x+5
hy−8x=5
For what value of h does the system of equations above have no solution?
View Solutioncx−5y=6
2x−3y=8
In the system of equations above, c is a constant and x and y are variables. For what values of c will the system have no solutions?
View Solution
