The figure above shows a regular hexagon with sides of length a and a square with sides of length a. If the area of the hexagon is 384 √3 square inches, what is the area, in square inches, of the square?
256
192
64√3
16√3
Choice A is correct. The regular hexagon can be divided into 6 equilateral triangles of side length a by drawing the six segments from the center of the regular hexagon to each of its 6 vertices. Since the area of the hexagon is 384√3 square inches, the area of each equilateral triangle will be 384√36=64√3 square inches.
Drawing any altitude of an equilateral triangle divides it into two 30°-60°-90° triangles. If the side length of the equilateral triangle is a, then the hypotenuse of each 30°-60°-90° triangle is a, and the altitude of the equilateral triangle will be the side opposite the 60° angle in each of the 30°-60°-90° triangles. Thus, the altitude of the equilateral triangle is √32a, and the area of the equilateral triangle is 12(a)(√32a)=√34a2. Since the area of each equilateral triangle is 64√3 square inches, it follows that a2=4√3(64√3)=256 square inches. And since the area of the square with side length a is a2, it follows that the square has area 256 square inches. Choices B, C, and D are incorrect and may result from calculation or conceptual errors
Similar Questions
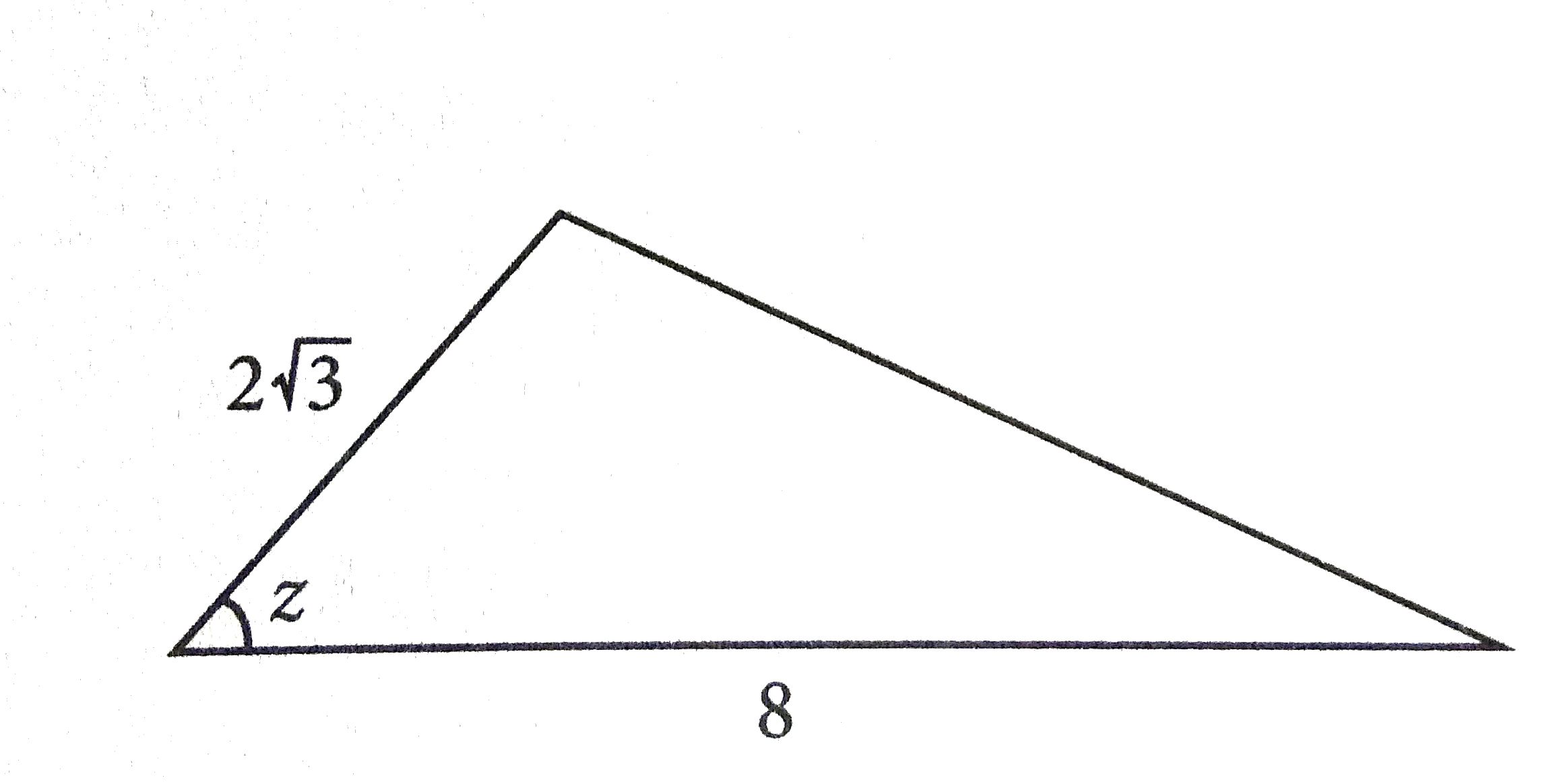
If the area of the triangle shown above is 12 squares inches, what is the value of cosz?
View SolutionIn the figure, the smaller square has sides of length 2 and the larger square has sides of length 4. If a point is chosen at random from the larger square, what is the probability that it will be from the small square?
View Solution
Knowledge Check
A circle has a radius that is the same length as the sides of a square , if the square has a perimeter of 64 square inches , what is the area , in square inches , of the circle ?
A16B16πC32πD256πA table screen has a 12-inch diagonal. If the length of the screen is √3 times longer than the width, what is the area, in square inches, of the screen ?
A12B12√3C36D36√3A triangle and a regular hexagon have the same perimeter. If the area of the hexagon is 72√3, what is the area of the triangle ?
A62.354B83.138C101.823D103.923
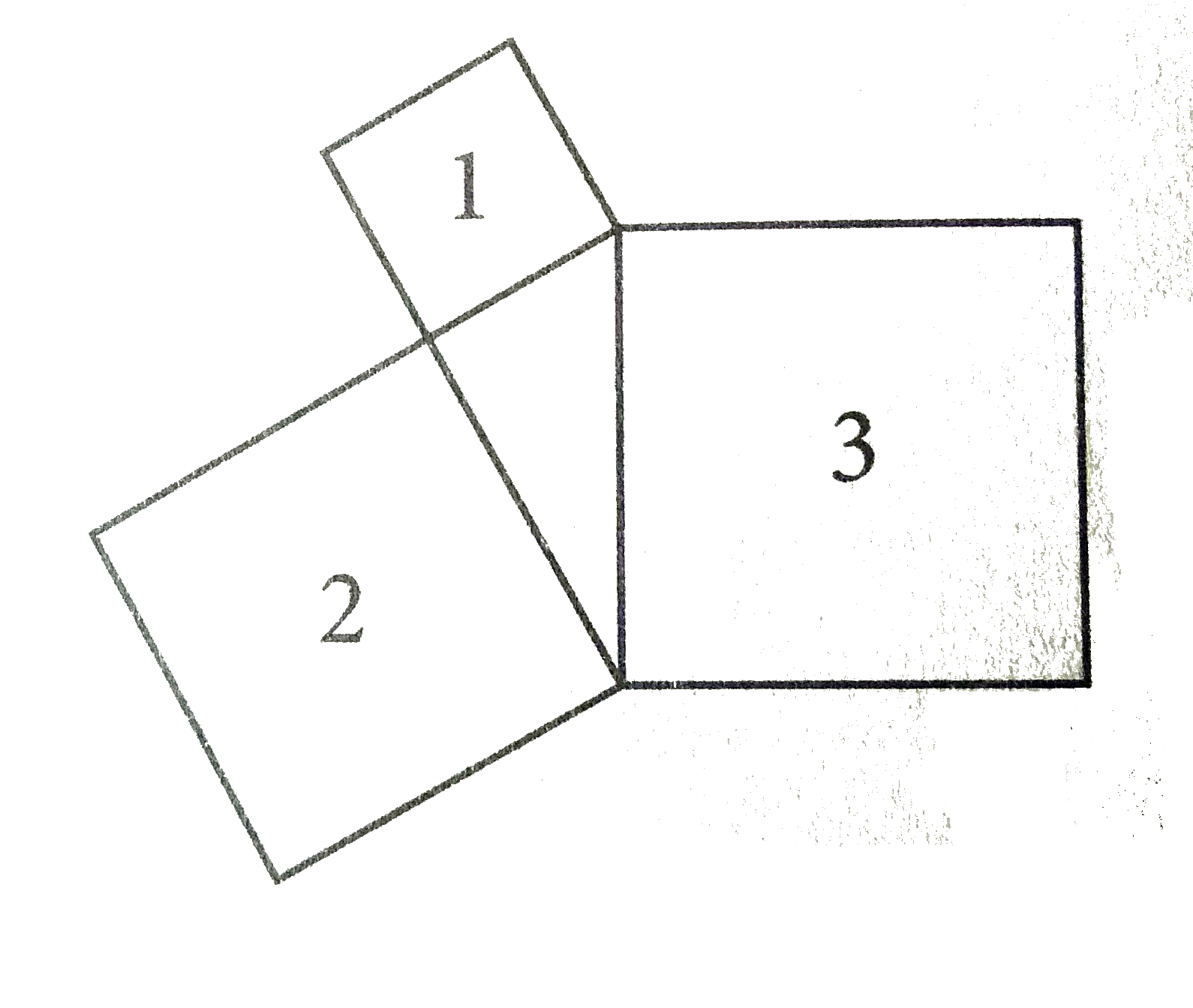
Each of the quadrilaterals figure above is a square. The area of the smallest square (square 1) is 16 square units, and the area of the medium square (square 2) is 48 square units. What is the area, in square units, of the largest square (square 3)?
View SolutionWhat is the area of a square whose sides are doubled?
View Solution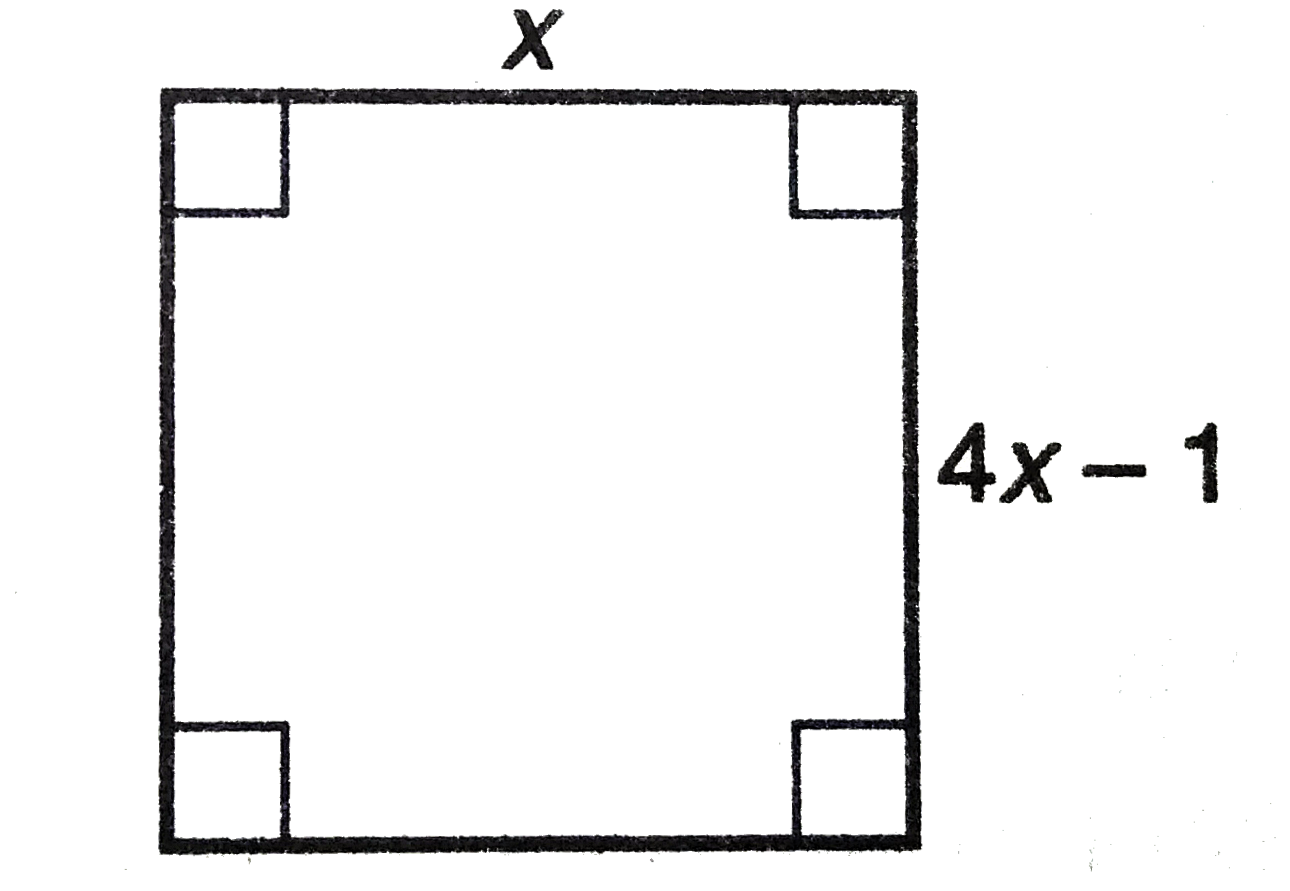
What is the area of the square above?
View SolutionThe perimeter of square is 36 inches . What is the area of the square , in square inches ?
View SolutionWhen each side of a given square is lengthened by 3 inches, the area is increased by 45 square inches. What is the length, in inches, of a sides of the original square?
View Solution
