Question

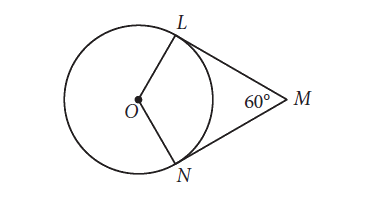
In the figure above, point O is the center of the circle, line segments LM and MN are tangent to the circle at points L and N, respectively, and the segments intersect at point M as shown. If the circumference of the circle is 96, what is the length of minor arc $\stackrel{⌢}{LN}$ ?

Explanation

The correct answer is 32. Since segments LM and MN are tangent to the circle at points L and N, respectively, angles OLM and ONM are right angles. Thus, in quadrilateral OLMN, the measure of angle O is 360° − (90° + 60° + 90°) = 120°. Thus, in the circle, central angle O cuts off `(120)/(360)=(1)/(3)` of the circumference, that is, minor arc`overset(frown)(LN)` is `(1)/(3)` of the circumference. Since the circumference is 96, the length of minor arc `overset(frown)(LN)` is `(1)/(3)xx 96 = 32.`