Question

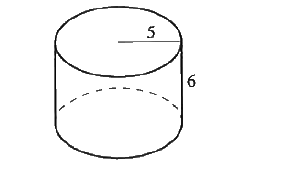
The volume of right circular cylinder A is 22 cubic centimeters. What is the volume , in cubic centimetres, of a right circular cylinder with twice the radius and half the height of cylinder A?

Options

A. 11
B. 22
C. 44
D. 66

Explanation

To solve the problem, we will follow these steps:

1. Understand the Volume Formula: The volume \( V \) of a right circular cylinder is given by the formula:
\( V = \pi r^2 h \)
where \( r \) is the radius and \( h \) is the height.

2. Set Up the Volume of Cylinder A: We know that the volume of cylinder A is 22 cubic centimeters. Therefore, we can write:
\( \pi r^2 h = 22 \)

3. Determine the Dimensions of the New Cylinder: The new cylinder has:
- Radius \( r_1 = 2r \) (twice the radius of cylinder A)
- Height \( h_1 = \frac{h}{2} \) (half the height of cylinder A)

4. Calculate the Volume of the New Cylinder: The volume \( V_1 \) of the new cylinder can be calculated using the formula:
\( V_1 = \pi r_1^2 h_1 \)
Substituting the values of \( r_1 \) and \( h_1 \):
\( V_1 = \pi (2r)^2 \left(\frac{h}{2}\right) \)

5. Simplify the Expression: Now, simplify the expression:
\( V_1 = \pi (4r^2) \left(\frac{h}{2}\right) \)
\( V_1 = \pi \cdot 4r^2 \cdot \frac{h}{2} = 2\pi r^2 h \)

6. Relate to the Volume of Cylinder A: We know from cylinder A that \( \pi r^2 h = 22 \). Therefore:
\( V_1 = 2 \cdot 22 = 44 \text{ cubic centimeters} \)

Thus, the volume of the new cylinder is 44 cubic centimeters.