Alan drives an average of 100 miles each week. His car can travel an average of 25 miles per gallon of gasoline. Alan would like to reduce his weekly expenditure on gasoline by $5. Assuming gasoline costs $4 per gallon, which equation can Alan use to determine how many fewer average miles,m, he should drive each week?
254m=95
254m=5
425m=95
425m=5
To solve the problem, we need to find an equation that Alan can use to determine how many fewer average miles he should drive each week in order to reduce his weekly expenditure on gasoline by $5.
1. Determine the current weekly gasoline expenditure:
- Alan drives 100 miles each week.
- His car travels 25 miles per gallon.
- Therefore, the number of gallons he uses in a week is:
Gallons used=Miles drivenMiles per gallon=10025=4 gallons
- The cost of gasoline is $4 per gallon, so his current expenditure is:
Expenditure=Gallons used×Cost per gallon=4×4=16 dollars
2. Set up the equation for reduced expenditure:
- Alan wants to reduce his expenditure by $5, so his new expenditure should be:
New expenditure=16−5=11 dollars
3. Express the new expenditure in terms of miles driven:
- Let m be the number of miles he drives less. Thus, the new distance driven will be 100−m.
- The gallons used for the new distance will be:
Gallons used=100−m25
- The new expenditure in terms of m will be:
New expenditure=(100−m25)×4
4. Set the new expenditure equal to the desired expenditure:
- We set the new expenditure equal to $11:
(100−m25)×4=11
5. Simplify the equation:
- Multiply both sides by 25 to eliminate the fraction:
4(100−m)=275
- Divide both sides by 4:
100−m=68.75
- Rearranging gives:
m=100−68.75=31.25
6. Final equation:
- To find the equation that Alan can use to determine how many fewer miles he should drive, we can express it as:
4m25=5
- This equation represents the relationship between the miles reduced and the savings in expenditure.
Final Answer:
The equation Alan can use is:
4m25=5
- Alan drives 100 miles each week.
- His car travels 25 miles per gallon.
- Therefore, the number of gallons he uses in a week is:
Gallons used=Miles drivenMiles per gallon=10025=4 gallons
- The cost of gasoline is $4 per gallon, so his current expenditure is:
Expenditure=Gallons used×Cost per gallon=4×4=16 dollars
- Alan wants to reduce his expenditure by $5, so his new expenditure should be:
New expenditure=16−5=11 dollars
- Let m be the number of miles he drives less. Thus, the new distance driven will be 100−m.
- The gallons used for the new distance will be:
Gallons used=100−m25
- The new expenditure in terms of m will be:
New expenditure=(100−m25)×4
- We set the new expenditure equal to $11:
(100−m25)×4=11
- Multiply both sides by 25 to eliminate the fraction:
4(100−m)=275
- Divide both sides by 4:
100−m=68.75
- Rearranging gives:
m=100−68.75=31.25
- To find the equation that Alan can use to determine how many fewer miles he should drive, we can express it as:
4m25=5
- This equation represents the relationship between the miles reduced and the savings in expenditure.
The equation Alan can use is:
4m25=5
Similar Questions
Jaime is preparing for a bicycle race. His goal is to bicycle an average of at least 280 miles per week for 4 weeks. He bicycled 240 miles the first week, 310 miles the second week, and 320 miles the third week. Which inequality can be used to represent the number of miles, x, Jaime could bicycle on the 4th week to meet his goal?
View SolutionThe scatterplot below compares the average gasoline prices I Boston, per gallon, to the average gasoline prices across the United States, per gallon, during a one-year period from 2017 to 2018.
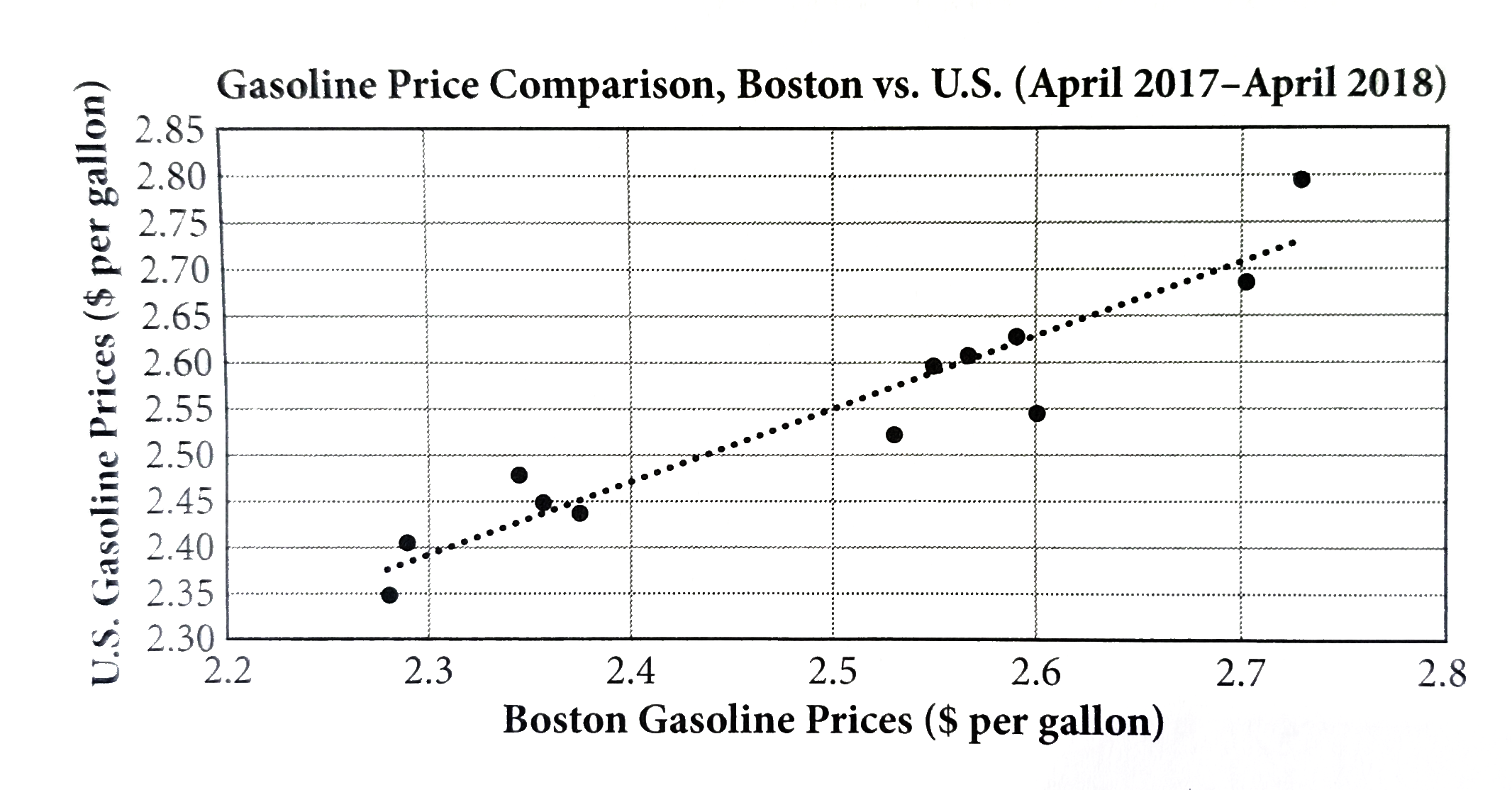
Of the following equations, whihc best modeles the data in the scatterplot ?
View SolutionA gas station sells regular gasoline for $2.39 per gallon and premium gasoline for $2.79 per gallon. If the gas station sold a total of 550 gallons of both types of gasoline in one day for a total of $1.344.50. how many gallons of premium gasoline were sold?
View SolutionOfficer Blake drives his squad car 1 mile per minute wile patrolling local highways during his shift. If he has driven 480 miles by the end of his shift, how many total hours did he drive his car at the above rate?
View SolutionJessica's car gets 18 miles per gallon when the car travels at an average speed of 35 miles per hour. Jessica begins a trip with 14 gallons of gas, and she travels at 35 miles per hour for the first 4 hours of her trip. Which of the following functions g is the most accurate model for the number of gallons of gallons of gas remaining in the tank t hours after the trip begins for 0≤t≤4?
View SolutionAn elephant traveled 7 miles at an average rate of 4 miles per hour and then traveled the next 7 miles at an average rate of 1 mile per hour. What was the average speed, in miles per hour, of the elephant for the 14 miles?
View SolutionA man motors from A to B. A large part of the distace is uphill and he gets a mileage of only 10 miles per gallon of gasoline. ON the return trip, he makes 15 miles per gallon, then the average of his mileage (assuming that the distance from A to B is 60 miles ) is
View Solution
