A psychologist set up an experiment to study the tendency of a person to select the first item when presented with a series of items. In the experiment, 300people were presented with a set of five pictures arranged in random order. Each person was asked to choose the most appealing picture. Of the first 150participants,36 chose the first picture in the set. Among the remaining 150 participants, p people chose the first picture in the set. If more than 20% of all participants chose the first picture in the set, which of the following in equalities best describes the possible values of p ?
p>0.20(300−36),wherep≤150
p>0.20(300+36),wherep≤150
p−36>0.20(300),wherep≤150
p+36gt0.20(300),where ple150'
To solve the problem step by step, we will analyze the information given and set up the necessary inequalities.
Step 1: Determine the total number of participants and the number who chose the first picture.
- We know that there are a total of 300 participants.
- From the first 150 participants, 36 chose the first picture.
- Let p be the number of participants from the second group of 150 who chose the first picture.
Step 2: Express the total number of participants who chose the first picture.
- The total number of participants who chose the first picture is:
36+p
Step 3: Calculate 20% of the total participants.
- We need to find out what 20% of 300 is:
0.2×300=60
Step 4: Set up the inequality.
- We are given that more than 20% of all participants chose the first picture. Therefore, we can set up the inequality:
36+p>60
Step 5: Solve the inequality for p.
- To isolate p, we subtract 36 from both sides:
p>60−36
p>24
Step 6: Determine the upper limit for p.
- Since p represents the number of participants from the second group of 150, it must also satisfy the condition:
p≤150
Step 7: Combine the inequalities.
- Therefore, we have the following compound inequality:
24<p≤150
Conclusion
The possible values of p that satisfy the conditions of the problem are:
p∈(24,150)
- We know that there are a total of 300 participants.
- From the first 150 participants, 36 chose the first picture.
- Let p be the number of participants from the second group of 150 who chose the first picture.
- The total number of participants who chose the first picture is:
36+p
- We need to find out what 20% of 300 is:
0.2×300=60
- We are given that more than 20% of all participants chose the first picture. Therefore, we can set up the inequality:
36+p>60
- To isolate p, we subtract 36 from both sides:
p>60−36
p>24
- Since p represents the number of participants from the second group of 150, it must also satisfy the condition:
p≤150
- Therefore, we have the following compound inequality:
24<p≤150
The possible values of p that satisfy the conditions of the problem are:
p∈(24,150)
Similar Questions
Knowledge Check
Study the picture given and choose the correct option:

The two main leaders in the picture are:AViceroy, Lord Irwin and Gandhiji.BJinnah and Gandhiji.CSir Stafford Cripps and GandhijiDSir Stafford Cripps and NehruStudy the picture and choose the correct name:
 AInclined plane methodBPersian wheel methodCMuscular methodDLever method
AInclined plane methodBPersian wheel methodCMuscular methodDLever method
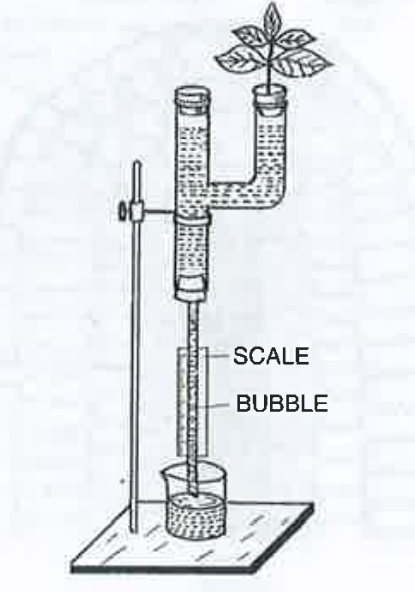
The experiment set up shown in the following diagram is for
View SolutionElectrons will first enter into the orbital with the set of quantum numbers
View SolutionThe experiment set up shown in the adjacent diagram is for

View SolutionThe person shown in the pictures is affected by a certain disease.

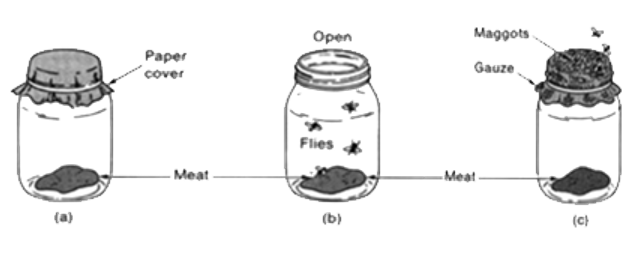
View SolutionObserve the picture below and state the name the of the scientist/s who performed this experiment ?
View SolutionLook at the picture, understand the experiment and answer the below related questions :
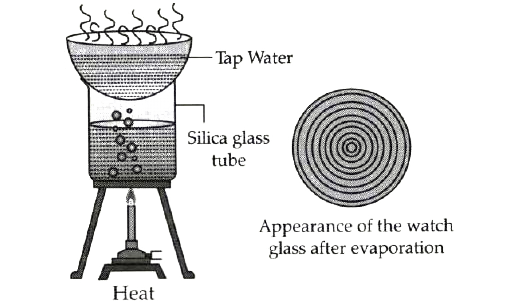
What is the aim of the experiment?
View Solution
