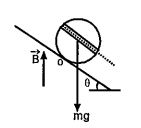
A non - conducting sphere has mass of 100 g and radius 20 cm . A flat compact coil of wire with turns 5 is wrapped tightly around it with each turns concentric with the sphere. This sphere is placed on an inclined plane such that plane of coil is parallel to the inclined plane.
A uniform magnetic field of 0.5 T exists in the region in vertically upwards direction. Compute the current I required to rest the sphere in equilibrium.
(##SURPHYXIIV01C03E04005_Q01##) Solution in Tamil
The sphere is in translational equilibrium , thus fs−mgsinθ = 0 ….(1)
The sphere is in rotational equilibrium . If torques are taken about the centre of the sphere, the magnetic field produces a clockwise torque of magnitude
i.e τ=mBsinq[μ=NIA]
The frictional force (fs) produces a anticlockwise torque of magnitude τ=fsR, where R is the radius of the sphere. Thus
fsR−mBsinθ=0 .....(2)
From (1) and (2) [i.e fs=mgsinθ substituting in (2)] mg sinθ.R−μBsinθmgR=μB
Substituting μ
mgR = NIAB
I=mgRNBA [where A is the area of the sphere A=πR2 ]
∴I=mgπRBN
Given :
mass of the sphere μ=100g=100×10−3kg
Radius of the sphere R=20cm=20×10−2m
No. of turns of wire wrapped N=5
Magnetic field B=0.5 T
Current required to rest the sphere in equilibrium I=?
I = (100 xx 10^(-3) xx cancel10^(2))/(pi xx cancel5 xx 20 xx 10^(-2) xx 0.5)
I=2πA
Similar Questions
1. A coil of area 2cm2 with turns 500 is placed in a magnetic field of 0.5 T with its plane parallel to field. The flux linked with the coil is
02:20View SolutionA circular coil of 25 turns and radius of 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of coil. If the current in the coil is 5 A, then total torque experienced by the coil is
02:32View SolutionA rectangular coil 20cm×20cm has 100 turns and carries a current of 1A. It is placed in a uniform magnetic field B=0.5T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
02:23View SolutionIn Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]
04:36View SolutionIn figure a coil of single turn is wound on a sphere of radius r and mass m the plane of the coil is parallel to the inclined plane and lies in the equatorial plan eof the sphere if thw sphere is in rotational equilibrium the value of B is:[current in the coil is]
View SolutionIn the figure shown a coil of single turn is wound on a sphere of radius r and mass m the plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere if sphere is nin rotational equilibrium the valu eof B is(current in the coil is)
 View Solution
View SolutionA rectangular coil 20cmxx20cm has 100 turns and carries a current of 1 A . It is placed in a uniform magnetic field B=0.5 T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
03:10View SolutionA rectangular coil 20cmxx20cm has 100 turns and carries a current of 1 A . It is placed in a uniform magnetic field B=0.5 T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
03:14View Solution

