A particle is projected with a velocity of 30ms−1, at an angle of θ0=tan−1(34). After 1s, the particle is moving at an angle θ to the horizontal, where tanθ will be equal to (Take, g=10ms−2)
1
2
12
13
The correct Answer is:D
To solve the problem step by step, we will follow the principles of projectile motion and trigonometry.
Step 1: Determine the initial components of velocity
The particle is projected with an initial velocity u=30m/s at an angle θ0=tan−1(34).
Using the definitions of sine and cosine:
- tanθ0=34
- This means that in a right triangle, the opposite side (perpendicular) is 3, and the adjacent side (base) is 4.
- The hypotenuse can be calculated using Pythagoras' theorem:
hypotenuse=√32+42=√9+16=5
From this, we can find:
- sinθ0=35
- cosθ0=45
Step 2: Calculate the horizontal and vertical components of the initial velocity
Using the initial velocity and the trigonometric functions:
- Horizontal component of velocity ux=ucosθ0=30⋅45=24m/s
- Vertical component of velocity uy=usinθ0=30⋅35=18m/s
Step 3: Determine the vertical velocity after 1 second
The vertical velocity changes due to gravity. The acceleration due to gravity g=10m/s2 acts downwards. After 1 second, the vertical velocity vy can be calculated as:
vy=uy−g⋅t=18−10⋅1=8m/s
Step 4: Determine the angle θ after 1 second
After 1 second, the horizontal velocity remains constant:
- vx=ux=24m/s
Now, we can find the angle θ that the resultant velocity makes with the horizontal:
tanθ=vyvx=824=13
Step 5: Conclusion
Therefore, the value of tanθ after 1 second is 13.
Final Answer
tanθ=13
---
The particle is projected with an initial velocity u=30m/s at an angle θ0=tan−1(34).
- tanθ0=34
- This means that in a right triangle, the opposite side (perpendicular) is 3, and the adjacent side (base) is 4.
- The hypotenuse can be calculated using Pythagoras' theorem:
hypotenuse=√32+42=√9+16=5
- sinθ0=35
- cosθ0=45
Using the initial velocity and the trigonometric functions:
- Horizontal component of velocity ux=ucosθ0=30⋅45=24m/s
- Vertical component of velocity uy=usinθ0=30⋅35=18m/s
The vertical velocity changes due to gravity. The acceleration due to gravity g=10m/s2 acts downwards. After 1 second, the vertical velocity vy can be calculated as:
vy=uy−g⋅t=18−10⋅1=8m/s
After 1 second, the horizontal velocity remains constant:
- vx=ux=24m/s
tanθ=vyvx=824=13
Therefore, the value of tanθ after 1 second is 13.
tanθ=13
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - B. Medical entrance1videos
MOTION
- BOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrance12videos
MOTION
- BOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - A. Taking it together1videos
MOTION
- BOOK - DC PANDEYCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective19videos
MEASUREMENT AND ERRORS
- BOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
Similar Questions
A particle is projected from the earth's surface with a velocity of 50 m s−1 at an angle θ with the horizontal. After 2s it just clears a wall 5m high. What is the value of 55sinθ?(g=10ms−2)
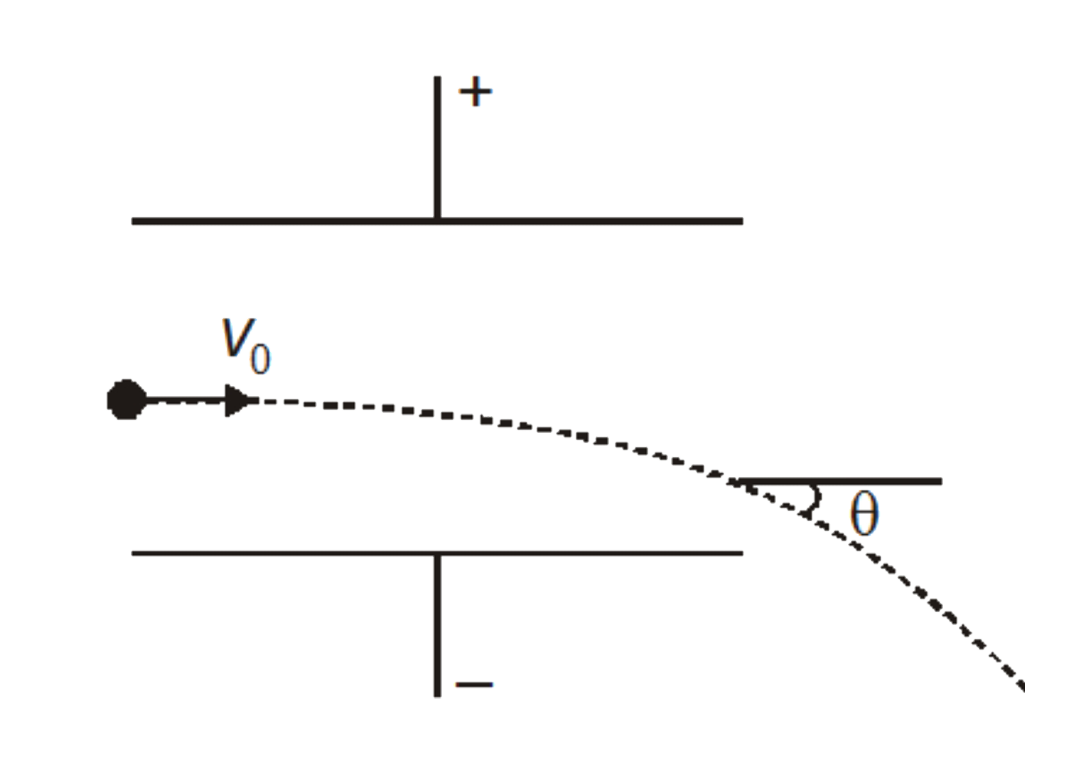
View Solutionwhen a positively charged particle is projected with a velocity v0 in the region between the horizontal plates of the capacitor then it leaves by making an angle θ with the horizontal , as shown. If θ=θ1 is for proton and θ=θ2 for an α - particle then the value of tanθ1tanθ2
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with a velocity of 30 m/s at an angle θ with the horizontal . Where θ=tan−1(34) . After 1 second, direction of motion of the particle makes an angle α with the horizontal then α is given by
Atanα=13Btanα=12Ctanα=2Dtanα=1 - Question 2 - Select One
A particle is projected at an angle of 45∘ with a velocity of 9.8ms−1. The horizontal range will be (Take, g=9.8ms−2)
A9.8mB4.9mC9.8√2D9.8√2 - Question 3 - Select One or More
A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
AAfter 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.BAfter 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.CThe magnitude of velocity of particle after 1 s is 10ms−1.DThe magnitude of velocity of particle after 1 s is 5ms−1.
If θ=60∘, then 1+tan2θ2tanθ is equal to
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionA ball is projected with a velocity 20√3ms−1 at angle 60∘ to the horizontal. The time interval after which the velocity vector will make an angle 30∘ to the horizontal is (Take, g=10ms−2)
View SolutionA body is projected horizontally with a velocity of ums−1 at an angle θ with the horizontal. The kinetic energy at the highest point is 34th of the kinetic energy. The value of θ is :
View Solution

