Electric charge of 1μC,−1μC and 2μC are placed in air at the corners A, B and C respectively of an equilateral triangle ABC having length of each side 10 cm. The resultant force on the charge at C is
0.9 N
1. 8N
2.7 N
3.6 N
The correct Answer is:B
To find the resultant force on the charge at point C due to the charges at points A and B, we can follow these steps:
Step 1: Identify the Charges and Their Positions
- Charge at A (qA) = +1 µC = +1 × 10^-6 C
- Charge at B (qB) = -1 µC = -1 × 10^-6 C
- Charge at C (qC) = +2 µC = +2 × 10^-6 C
- The distance between each pair of charges (length of sides of the triangle) = 10 cm = 0.1 m.
Step 2: Calculate the Force on Charge C due to Charge A
Using Coulomb's Law:
FCA=k|qC⋅qA|r2
Where:
- k (Coulomb's constant) = 9×109N m2/C2
- r = 0.1 m
Substituting the values:
FCA=9×109(2×10−6)(1×10−6)(0.1)2
FCA=9×109(2×10−12)0.01
FCA=9×109×2×10−10
FCA=1.8N
Step 3: Calculate the Force on Charge C due to Charge B
Again using Coulomb's Law:
FCB=k|qC⋅qB|r2
Substituting the values:
FCB=9×109(2×10−6)(1×10−6)(0.1)2
Since qB is negative, this force will be attractive:
FCB=9×109(2×10−12)0.01
FCB=9×109×2×10−10
FCB=1.8N
Step 4: Determine the Direction of Forces
- FCA (due to charge A) is repulsive and directed away from A towards C.
- FCB (due to charge B) is attractive and directed towards B.
Step 5: Calculate the Resultant Force
The angle between FCA and FCB is 120 degrees (since the triangle is equilateral). We can use the law of cosines to find the resultant force FR:
F2R=F2CA+F2CB+2FCAFCBcos(120∘)
Since cos(120∘)=−0.5:
F2R=(1.8)2+(1.8)2+2(1.8)(1.8)(−0.5)
F2R=3.24+3.24−3.24
F2R=3.24
FR=√3.24
FR≈1.8N
Final Result
The resultant force on the charge at C is approximately 1.8 N.
---
- Charge at A (qA) = +1 µC = +1 × 10^-6 C
- Charge at B (qB) = -1 µC = -1 × 10^-6 C
- Charge at C (qC) = +2 µC = +2 × 10^-6 C
- The distance between each pair of charges (length of sides of the triangle) = 10 cm = 0.1 m.
Using Coulomb's Law:
FCA=k|qC⋅qA|r2
Where:
- k (Coulomb's constant) = 9×109N m2/C2
- r = 0.1 m
FCA=9×109(2×10−6)(1×10−6)(0.1)2
FCA=9×109(2×10−12)0.01
FCA=9×109×2×10−10
FCA=1.8N
Again using Coulomb's Law:
FCB=k|qC⋅qB|r2
Substituting the values:
FCB=9×109(2×10−6)(1×10−6)(0.1)2
Since qB is negative, this force will be attractive:
FCB=9×109(2×10−12)0.01
FCB=9×109×2×10−10
FCB=1.8N
- FCA (due to charge A) is repulsive and directed away from A towards C.
- FCB (due to charge B) is attractive and directed towards B.
The angle between FCA and FCB is 120 degrees (since the triangle is equilateral). We can use the law of cosines to find the resultant force FR:
F2R=F2CA+F2CB+2FCAFCBcos(120∘)
Since cos(120∘)=−0.5:
F2R=(1.8)2+(1.8)2+2(1.8)(1.8)(−0.5)
F2R=3.24+3.24−3.24
F2R=3.24
FR=√3.24
FR≈1.8N
The resultant force on the charge at C is approximately 1.8 N.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.3
10 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.1
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
Charges of +5μC,+10μC and −10μC are placed in air at the corners A,B and C of an equilateral triangle ABC, having each side equal to 5 cm. Determine the resultant force on the charge at A.
View SolutionCharges of +4μC,−6μCand−16μC are placed in air at the corners of an equilateral triangle of side 10. find the potential energy of the system. −0.72J
View Solution
Knowledge Check
Electric charges of 1μC,−1μC and 2μC are placed in air at the corners A,B and C respectively of an equilateral triangle ABC having length of each side 10cm. The resultant force on the charge at C is
A0.9NB1.8NC2.7ND3.6NElectric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
A1.8 VB1.8×106VC1.8×105VD1.8×104VCharge of 5μC each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is :-
A78 NB39 NC29 ND22.5 N
Three point charges of +2μC,−3μC , and −3μC are kept at the vertices A, B, and C, respectively of an equilatreral triangle of side 20 cm. what should be the sign and magnitude of the charge (q) to be placed at the midpoint (M) of side BC so that the charge at A remains in equilibrium?
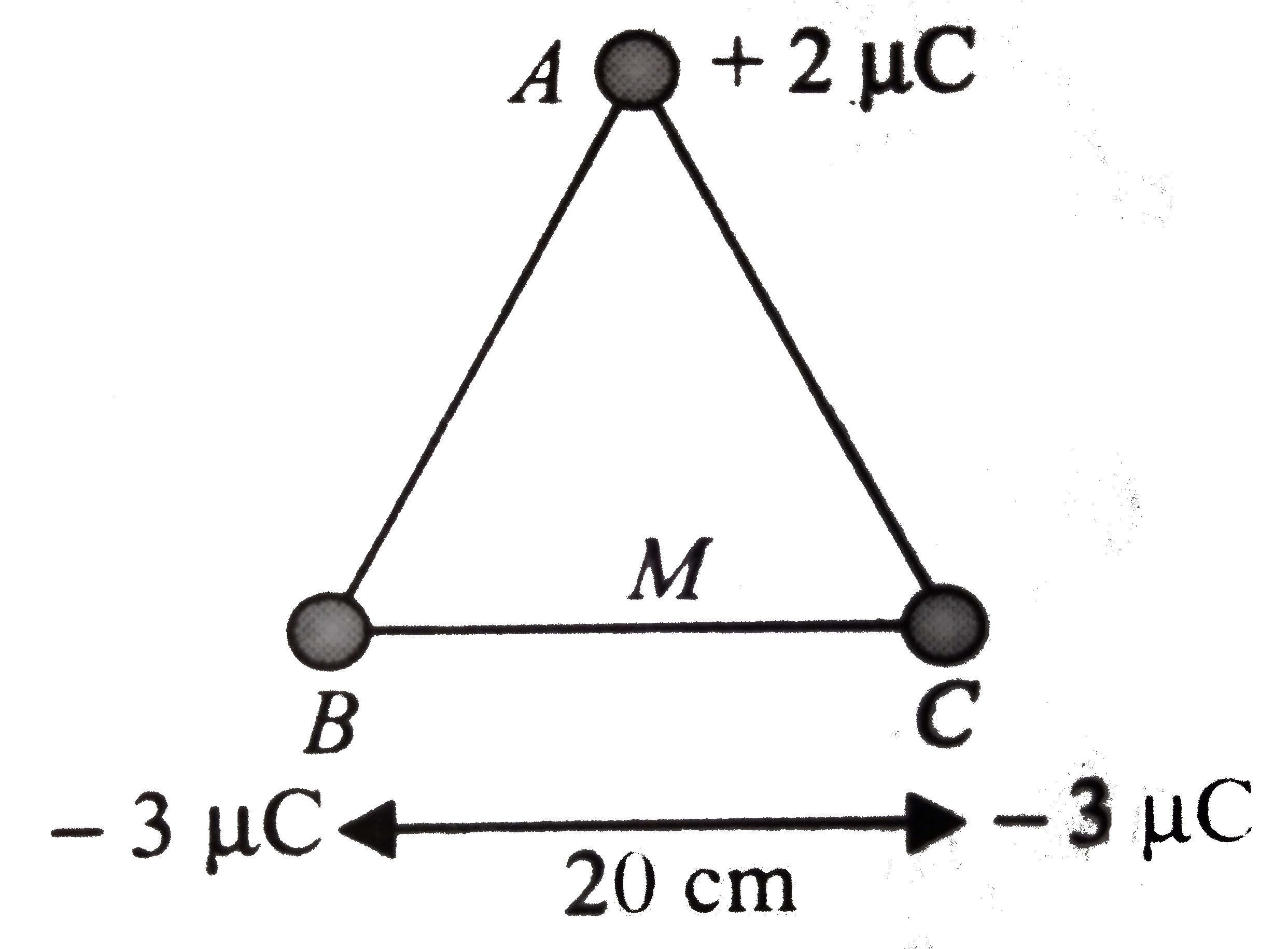
View SolutionThree point charges of +2μC,−3μCand−3μC are kept at the vertices A,B and C , respectively of an equilateral triangle of side 20 cm as shown in What should be the sign and magnitude of the charge to be placed at the mid-point (M) of side BC so that the charge at A remains in equilibrium?
(##U_LIK_SP_PHY_XII_C01_E09_017_Q01.png" width="80%">
View SolutionThree point charges 2μC,3μCand5μC are placed at the corners of an equilateral triangle of side 200 cm. Calculate the potentail energy of the system.
View SolutionThree charges +Q each are placed at the corners A,B and C of an equilateral triangle. At the circumcenre, O the electric field wil be

View SolutionThree charges 4μC,4μCand−4μC are placed at vertices of an equilateral triangle of side length 20cm. The potential centre is nearly.
View Solution
