Three equal charges are placed on the three corners of a square. If the force between q1 and q2 is F12 and that between q1 and q3 is F13, then the ratio of magnitudes (F12/F13) is
1/2
2
1/√2
√2
The correct Answer is:B
To solve the problem, we need to find the ratio of the magnitudes of the forces F12 and F13 between three equal charges q1, q2, and q3 placed at the corners of a square.
1. Understanding the Configuration:
- We have three equal charges q placed at the corners of a square. Let's denote the side length of the square as A.
- The charges are positioned as follows:
- q1 at (0, 0)
- q2 at (A, 0)
- q3 at (0, A)
2. Calculating the Force F12:
- The force F12 is the electrostatic force between charges q1 and q2.
- The distance between q1 and q2 is A.
- Using Coulomb's law, the force is given by:
F12=k⋅q1⋅q2A2
- Since q1=q2=q, we have:
F12=k⋅q2A2
3. Calculating the Force F13:
- The force F13 is the electrostatic force between charges q1 and q3.
- The distance between q1 and q3 is the diagonal of the square, which can be calculated using the Pythagorean theorem:
Distance=√A2+A2=A√2
- Using Coulomb's law, the force is given by:
F13=k⋅q1⋅q3(A√2)2
- Since q1=q3=q, we have:
F13=k⋅q22A2
4. Finding the Ratio F12F13:
- Now we can find the ratio of the forces:
F12F13=k⋅q2A2k⋅q22A2=112=2
5. Final Result:
- Therefore, the ratio of the magnitudes of the forces is:
F12F13=2
- We have three equal charges q placed at the corners of a square. Let's denote the side length of the square as A.
- The charges are positioned as follows:
- q1 at (0, 0)
- q2 at (A, 0)
- q3 at (0, A)
- The force F12 is the electrostatic force between charges q1 and q2.
- The distance between q1 and q2 is A.
- Using Coulomb's law, the force is given by:
F12=k⋅q1⋅q2A2
- Since q1=q2=q, we have:
F12=k⋅q2A2
- The force F13 is the electrostatic force between charges q1 and q3.
- The distance between q1 and q3 is the diagonal of the square, which can be calculated using the Pythagorean theorem:
Distance=√A2+A2=A√2
- Using Coulomb's law, the force is given by:
F13=k⋅q1⋅q3(A√2)2
- Since q1=q3=q, we have:
F13=k⋅q22A2
- Now we can find the ratio of the forces:
F12F13=k⋅q2A2k⋅q22A2=112=2
- Therefore, the ratio of the magnitudes of the forces is:
F12F13=2
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason15videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Match the columns5videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.520videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions120videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
Three identical charges are placed on three vertices of a square. If the force acting between q1andq2 is F12 and between q1andq3 is F13 then F13F12= ________.
A12B2C1√2D√2 - Question 2 - Select One
Equal charges q are placed at the three corners B, C, D of a square ABCD of side 'a'. The ratio of potential at A to centre O is
A2√2+13√2B2+√26C2√2+16D2√2+13 - Question 3 - Select One
Four charges +Q,−Q,+Q,−Q are placed at the corners of a square taken in order. At the centre of the square
AE=0,V=0BE=0,V≠0CE≠0,V=0DE=0,V≠0
Equal charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View SolutionThree equal charges Q are placed at the three corners of an equilateral triangle of side length a. Work done in shifting a charge q from infinity to the centroid of the triangle is
View SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
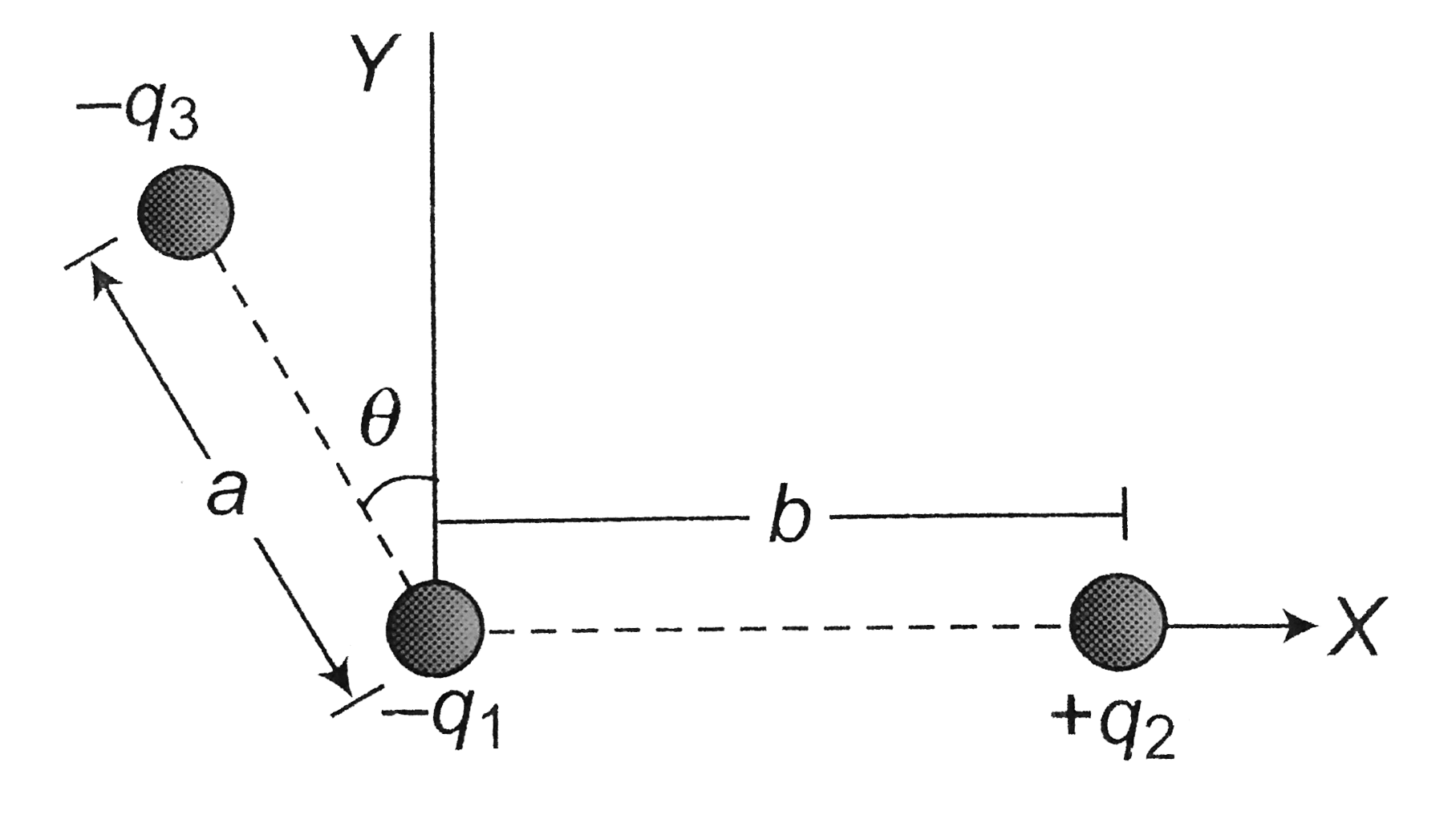 View Solution
View SolutionThree charges −q1, +q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
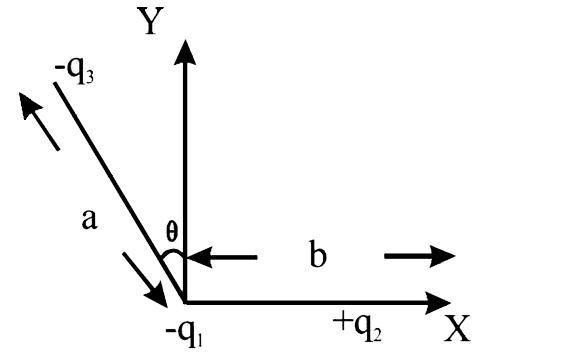 View Solution
View SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
 View Solution
View Solution

