Assertion : If a dipole is enclosed by a surface, then according to Gauss's law, electric flux linked with it will be zero.
Reason : The charge enclosed by a surface is zero.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
If Assertion is true but Reason is false
If Assertion is false but Reason is true
The correct Answer is:A
Step by step video, text & image solution for Assertion : If a dipole is enclosed by a surface, then according to Gauss's law, electric flux linked with it will be zero. Reason : The charge enclosed by a surface is zero. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Match the columns5videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Taking it together105videos
ELECTROSTATICS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions120videos
GRAVITATION
Similar Questions
Knowledge Check
- Question 1 - Select One
Assertion: No net charge can exist in the region where electric field is uniform.
Reason: For any type of Gaussian surface selected within the region of a uniform electric field, the angle between electric field intensity and area normal is 90∘ everywhere. Hence, electric flux linked with the selected Gaussian surface is equal to zero. If the net electric flux is zero for some Gaussian surface then according to Gauss's law the net charge enclosed within the surface must be zero.AIf both assertion and reason are correct and reason is a correct explanation of the assertion .BIf both assertion and reason are correct but reason is not the correct explanation of assertionCIf assertion is correct but reason is incorrectDIf assertion is incorrect but reason is correct. - Question 2 - Select One
Assertion(A):If Gaussian surface does not enclose any charge then →E at any point on the Gaussian surface must be zero.
Assertion(R ):No net charge is enclosed by Gaussians surface,so net flux passing through the surface is zero.ABoth A and R are true and R is the correct explanation of ABBoth A and R are True but R is not the correct explanation of A.CA is true and R is falseDA is false and R is true. - Question 3 - Select One
Answer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
What is the electrical flux through a cube of side 'a' if a point charge 'q' is placed at one of its vertices?Aq∈0B2q∈0Cq8∈0Dq∈0.6a2
Which of the following statement is correct ? If E = 0 , at all points of a closed surface.
a. the electirc flux through the surface is zero.
b. the total charge enclosed by the surface is zero.View SolutionIf net charge enclosed by a Gaussian surface is zero, then
Assertion :- →E at any point on Gaussian surface is 0.
Reason :- No net charge is enclosed by Gaussian surface, so E = 0View SolutionAnswer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
A charge q is enclosed by a Gaussian spherical surface of raidus R. If the radius is doubled then the electric flux will.View SolutionA charge q is enclosed as shown, below the electric flux is
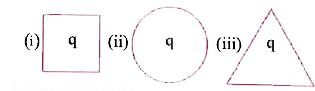 View Solution
View SolutionWhich of the following law gives a relation between the electric flux through any closed surface and the charge enclosed by the surface ?
View Solution

