In the given figure, there are four point charges placed at the vertices of a square of side, . If m then find the electric at the centre P of the square Assume the potential to be zero at infinity.

Step by step video & image solution for In the given figure, there are four point charges placed at the vertices of a square of side, a=1.4 m. If q_(1)=+18 nC,q_(2)=-24 nC,q_(3)+35nC and q_(4)=+16 nCm then find the electric at the centre P of the square Assume the potential to be zero at infinity. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
charges of 20nC each are placed at the corners A and B of a square ABCD of side √8cm and charges of −10nC at the corners C and D. find the potential at the centre of the square.
View SolutionIn Fig., the four particles form a square of edge length a = 5.00 cm and have charges q1=+3nC,q2=−15nC,q3=+15nC, and q4=−30nC. In unit-vector notation, what net electric field do the particles produce at the square's center ?

View Solution
Knowledge Check
Three charges are placed at the vertices of an equilateral triangle of side 10 cm. Assume q1=1μC,q2=−2μCandq3=4μC. Work done in separating the charges to infinity is
A−4.5JB4.5JC45 JDNone of theseFour charges Q-Q, Q-Q are placed at the corners of a square as shown . The potential is zero at points
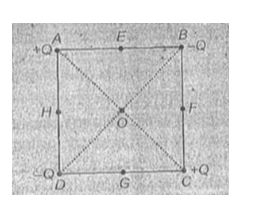 AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO only
AE,F,G,H,OBE,O,G onlyCH,O,F onlyDO onlyThree point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2
Four charges q1=1μC,q2=2μC,q3=−3μCandq4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.

View SolutionFour identical charges q are kept on each vertices of a square of side a. Calculate the extra amount of work done in bringing a Q charge from infinity to the centre of the square.
View SolutionPositive charges of 6,12 and 24 nC are placed at the thre vertices of a square. What charge must be placed at fourth vertex so that total potential at the centre of the square is zero?
View Solution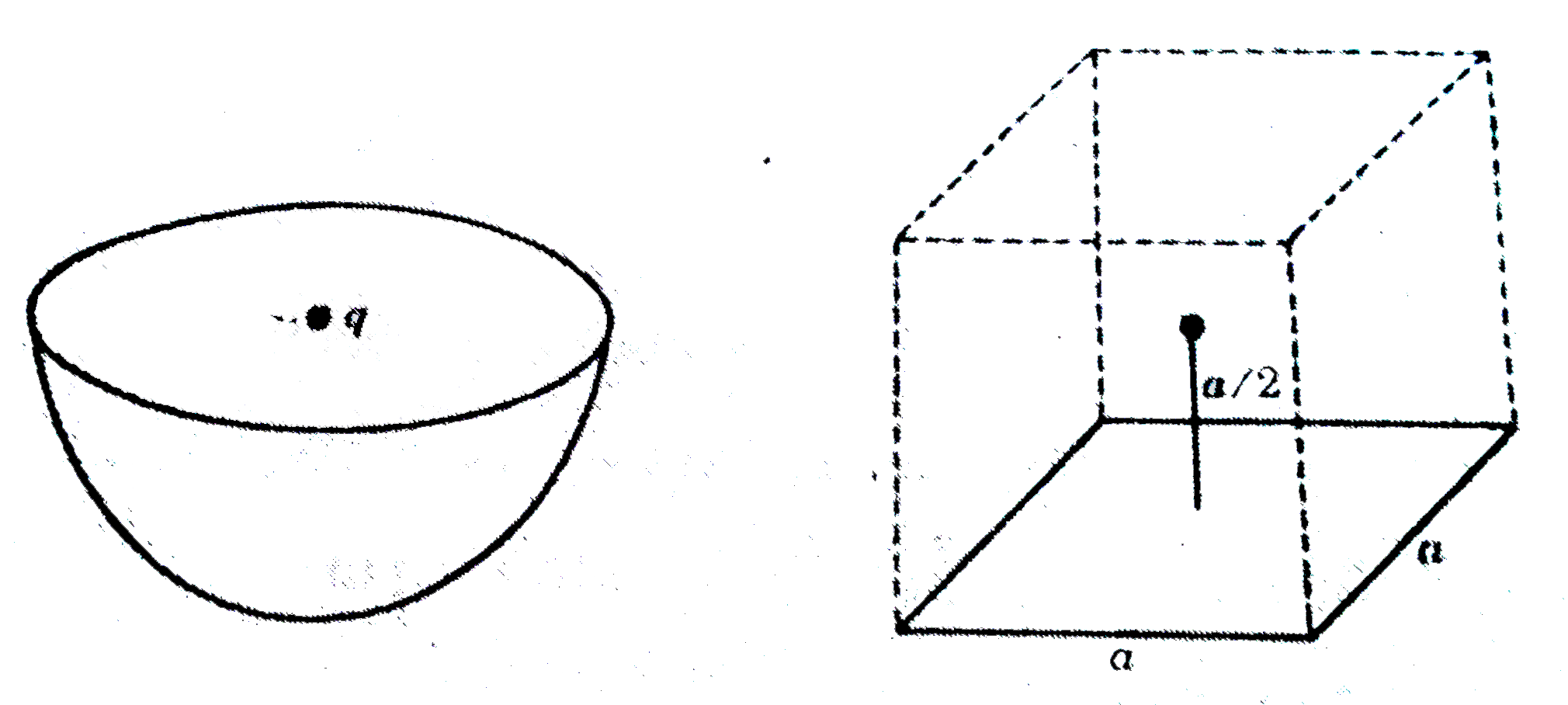
A point charge q is placed at a distnace a/2 directly above the centre of a square of side a, as shown figure. Find the magnitude of the electric flux through the square.
View SolutionFour identical charges i.e. q is placed at the corners of a square of side a. The charge Q that must be placed at the centre of the square such that the whole system of charges in equilibrium is
View Solution
