If the charge on a capacitor is increased by 2C, then the energy stored in it increases by 21 %. The original charge on the capacitor is
10 C
20 C
30 C
40 C
The correct Answer is:B
To solve the problem, we need to find the original charge on the capacitor given that an increase of 2C in charge results in a 21% increase in the energy stored in the capacitor.
1. Understand the relationship between charge and energy:
The energy (U) stored in a capacitor is given by the formula:
U=q22C
where q is the charge and C is the capacitance.
2. Set up the equation for the initial energy:
Let the initial charge on the capacitor be q. The initial energy stored in the capacitor is:
Ui=q22C
3. Determine the new charge and energy:
When the charge is increased by 2C, the new charge becomes:
qf=q+2
The new energy stored in the capacitor is:
Uf=(q+2)22C
4. Express the percentage increase in energy:
According to the problem, the energy increases by 21%, so we can write:
Uf=Ui+0.21Ui=1.21Ui
Substituting the expressions for Uf and Ui:
(q+2)22C=1.21(q22C)
5. Eliminate the common factor:
Since 12C is common on both sides, we can cancel it out:
(q+2)2=1.21q2
6. Expand and rearrange the equation:
Expanding the left side:
q2+4q+4=1.21q2
Rearranging gives:
0=1.21q2−q2−4q−4
Simplifying:
0=0.21q2−4q−4
7. Multiply through by 100 to eliminate decimals:
0=21q2−400q−400
8. Use the quadratic formula:
The quadratic formula is given by:
q=−b±√b2−4ac2a
Here, a=21, b=−400, and c=−400:
q=400±√(−400)2−4⋅21⋅(−400)2⋅21
9. Calculate the discriminant:
=400±√160000+3360042
=400±√19360042
=400±44042
10. Find the two possible solutions:
- First solution:
q=84042=20
- Second solution:
q=−4042 (not physically meaningful)
11. Conclusion:
The original charge on the capacitor is:
q=20C
The energy (U) stored in a capacitor is given by the formula:
U=q22C
where q is the charge and C is the capacitance.
Let the initial charge on the capacitor be q. The initial energy stored in the capacitor is:
Ui=q22C
When the charge is increased by 2C, the new charge becomes:
qf=q+2
The new energy stored in the capacitor is:
Uf=(q+2)22C
According to the problem, the energy increases by 21%, so we can write:
Uf=Ui+0.21Ui=1.21Ui
Substituting the expressions for Uf and Ui:
(q+2)22C=1.21(q22C)
Since 12C is common on both sides, we can cancel it out:
(q+2)2=1.21q2
Expanding the left side:
q2+4q+4=1.21q2
Rearranging gives:
0=1.21q2−q2−4q−4
Simplifying:
0=0.21q2−4q−4
0=21q2−400q−400
The quadratic formula is given by:
q=−b±√b2−4ac2a
Here, a=21, b=−400, and c=−400:
q=400±√(−400)2−4⋅21⋅(−400)2⋅21
=400±√160000+3360042
=400±√19360042
=400±44042
- First solution:
q=84042=20
- Second solution:
q=−4042 (not physically meaningful)
The original charge on the capacitor is:
q=20C
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (A) Chapter exercises
229 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.4
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Knowledge Check
The charge on a 48 μF capacitor is increased from 0.1 C to 0.5 C. the enerrgy stored in the capacitor increases by
A250 JB2500 JC2.5×106JD2.42×10−6JIf a 4μF capacitor is charged to 1KV, then energy stored is conductor is
A1JB8JC4JD2JIf a 4μF capacitor is charged to 1 kV, then energy stored in the capacitor is
A1 JB4 JC6 JD2 J
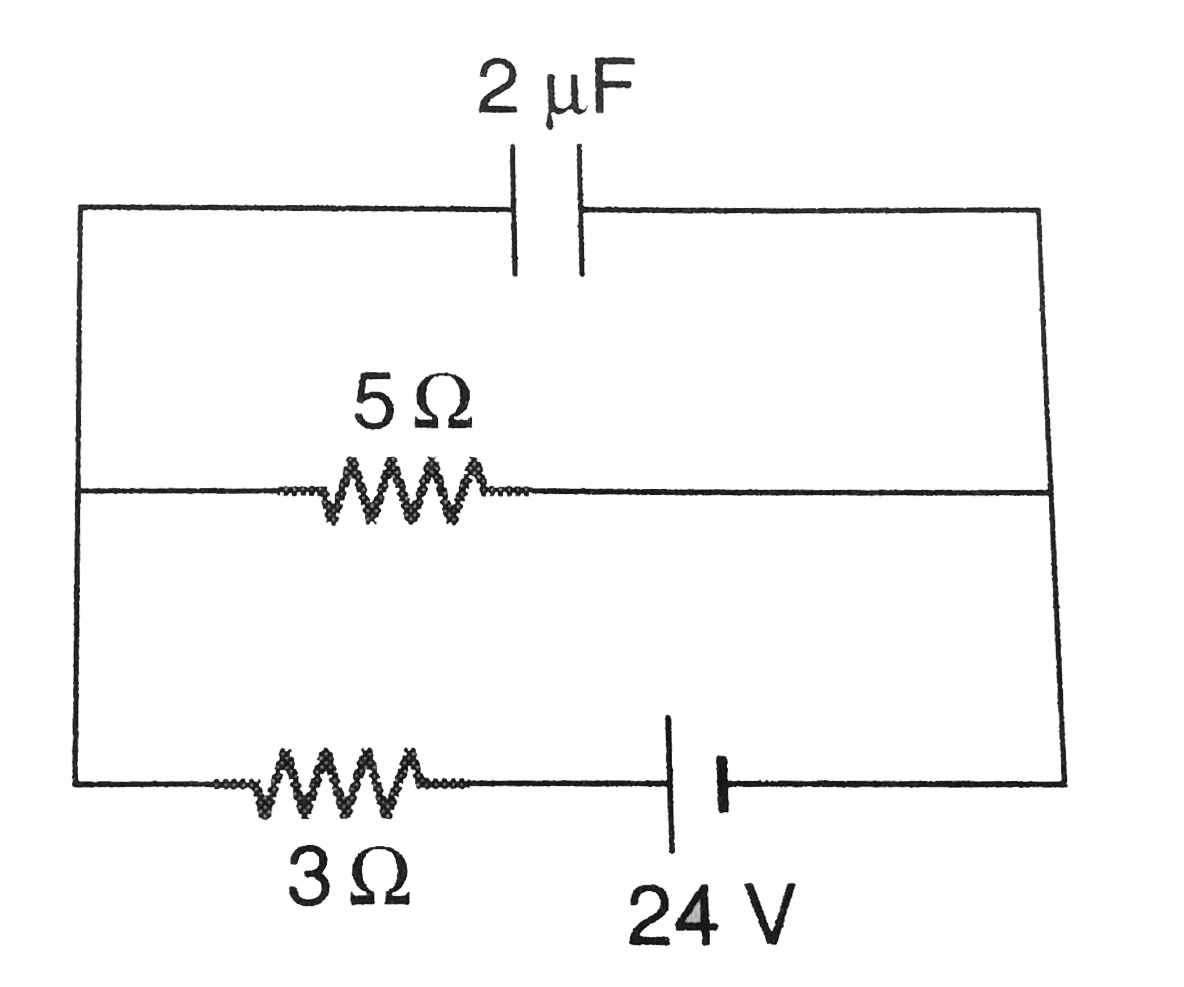
Find the charge stored in the capacitor.
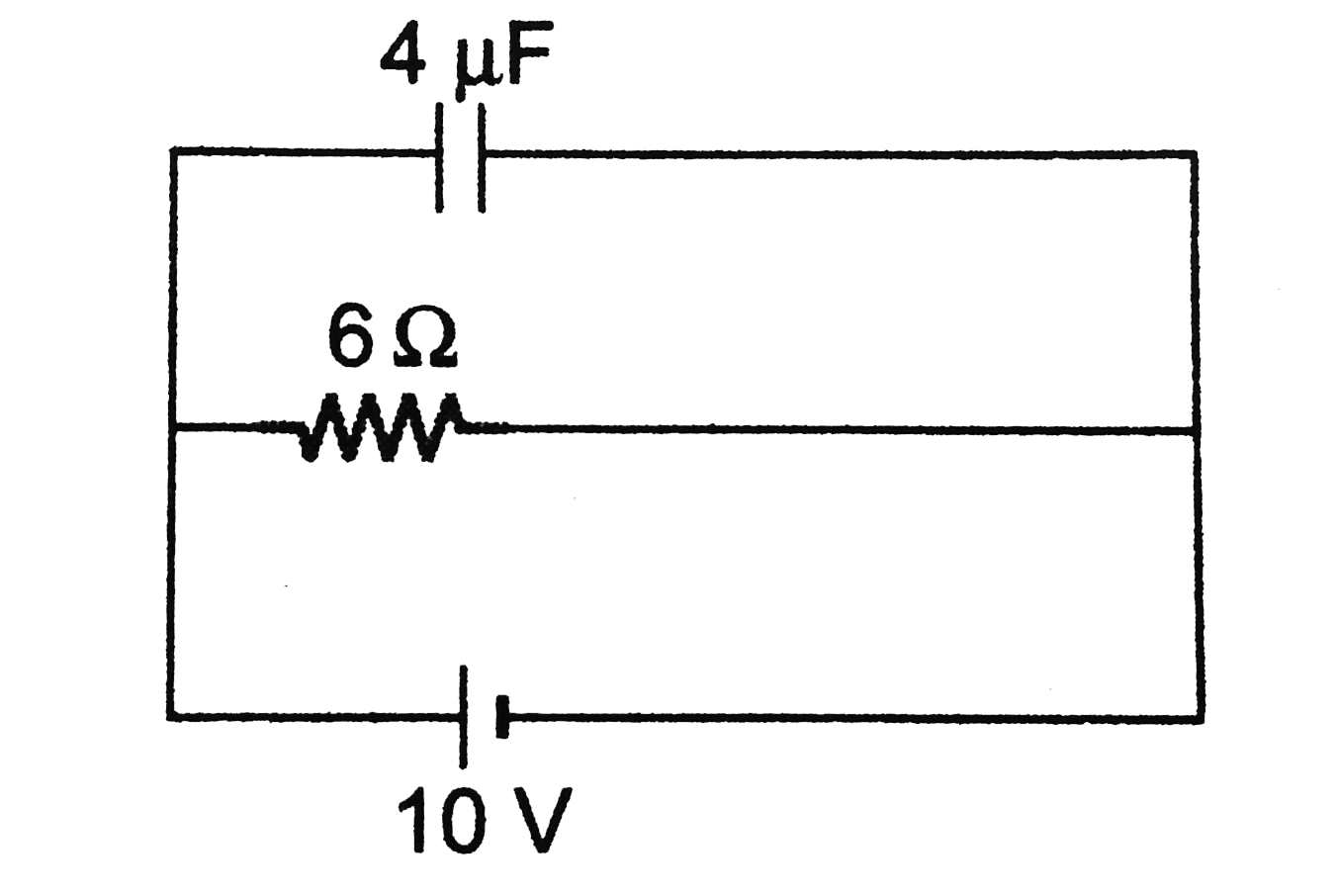
View SolutionFind the charge stored in the capacitor.
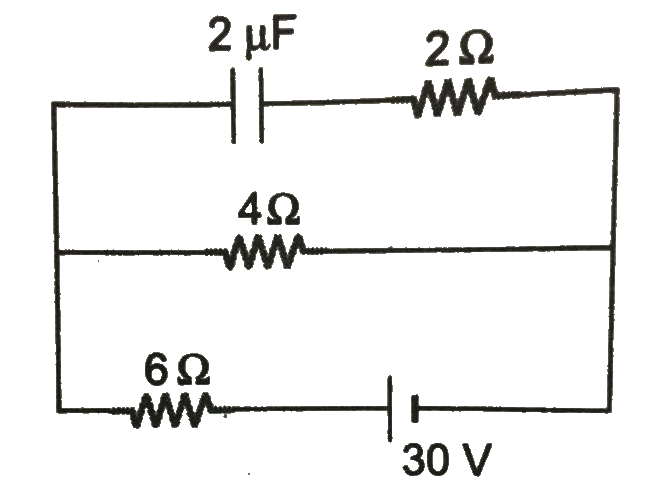
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
View SolutionThe heat produced by a resistor in any time t during the charging of a capacitor in a series circuit is half the energy stored in the capacitor by that time.
Current in the circuit is equal to the rate of increase in charge on the capacitor.
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View Solution