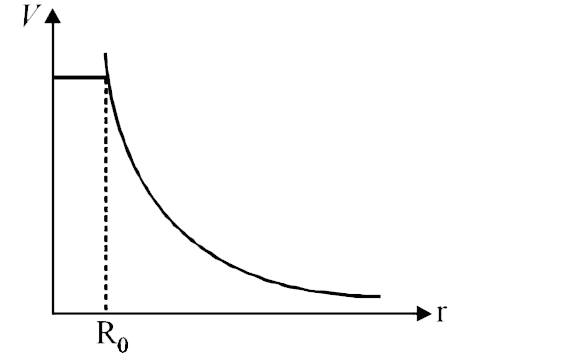
The electrostatic potential ϕr, of a spherical symmetrical system kept at origin, is shown in the adjacent figure, and given as
ϕr=q4πε0r(r≥R0)
ϕr=q4πε0R0(r≤R0)
Which of the following option is incorrect ?

For spherical region r≤R0 total electrostatic energy stored is zero
With in r=2R0, total charge is q/2
There will be no charge anywhere except at r = R
Electric field is discontinuous at r=R0
The correct Answer is:B
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
View SolutionFor spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View Solution
Knowledge Check
The electrostatic potential (ϕr) of a spherical symmetric system , kept at origin is shown in the adhacent figure, and given as
ϕe=q4πɛ0r(r≤Ro)
ϕe=q4πɛ0Ro(r≤R0)

Which of the following option s in //are correct ?AFor spherical region r≤R0 total electrostatic energy stored id zero .BWithin r=2R0, total charge is q.CThere will be no charge anywhere except at r=R0.DElectric field is discontinuous at r=R0.A spherical symmetric charge system is centered at origin. Given, Electric potential
V=Q4πε0R0(r≤R0), V=Q4πε0r(r>R0)
 A(a) Within r=2R0 total enclosed net charge is QB(b) Electric field is discontinued at r=R0C(c) Charge is only present at r=R0D(d) Electrostatic energy is zero for r<R0
A(a) Within r=2R0 total enclosed net charge is QB(b) Electric field is discontinued at r=R0C(c) Charge is only present at r=R0D(d) Electrostatic energy is zero for r<R0A conducting sphere A of radius a, with charge Q, is placed concentrically inside a conducting shell B of radius b. B is earthed. C is the common center of AandB. Study the following statements.
(i) The potential at a distance r from C, where
a≤r≤b,is14πε0(qr)
(ii) The potential difference between AandB is
14πε0Q(1r−1B)
(iii) The potential at a distance r from C, where
a≤r≤b,is14πε0Q(1r−1B)
Which of the above statements are correct ?
 .AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of these
.AOnly (i) and (ii)BOnly (ii) and (iii)COnly (i) and (iii)DAll of these
For spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View SolutionThe graph of a quadratic polynomial y=px2−qx+r is as shown in the adjacent figure, then (i)r2−4q<0 (ii)r2−4p<0 (iii) p+q>0 (iv) r−p−q>0
View SolutionShow that electric potential at a point P, at a distance .r. from a fixed point charge Q, is given by :
V=(14πε0)Qr
View Solution41.Self energy of conducting sphere of radius r carrying charge is (1) Q28πε0(r) (2) Q24πε0(r) (3) Q26πε0(r) (4) Q22πε0(r)
View SolutionA ball of radius R carries a positive charge throughout its volume, such that the volume density of charge depends on distance r from the ball's centre as ρ=ρ0(1−r®), where ρ0 is a constant. Assuming the permittivity of ball to be one , find magnitude of electric field as a function of distance r, both inside and outside the ball.
Strategy : The field has a spherical symmetry . For a point outside the ball (r>R)
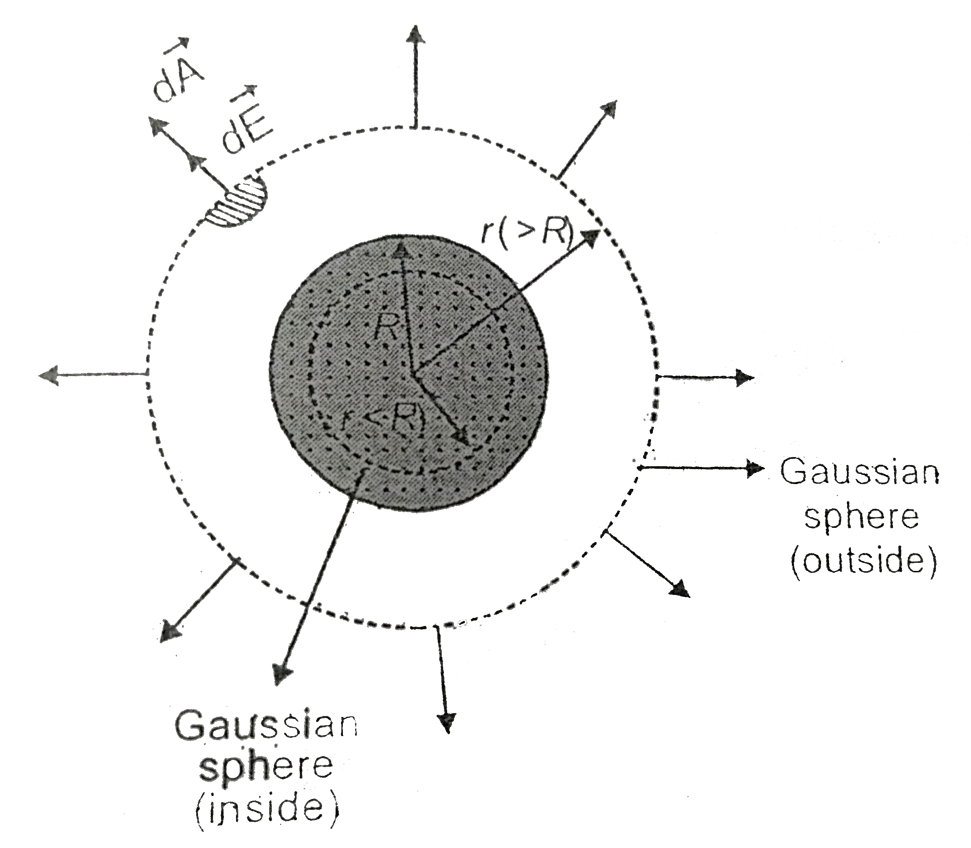
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law , ϕ=Qε0
⇒Eout=Q4πε0r2, where Q is total charge
For a point inside the ball (r<R)
ϕ=∮→E.¯¯¯¯¯dA=E×4πr2
By Gauss law, ϕ=qencε0
⇒Ein=qenc4πε0r2
where qenc= charge in a sphere of radius r(<R)
To find the enclosed charge , consider a spherical shell of radius r and thickness dr
Its volume dV=4πr2dr
Charge dq=ρdV
⇒dq=ρ0(1−rR)4πr2dr
⇒q=∫r0ρ0(1−rR)4πr2dr
=ρ04π[∫r0r2dr−∫r0r3Rdr]=ρ04π[r33−r44R]

View Solution
