A projectile of mass m, charge Z', initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters .show that for b=0, s reduces to the closest distance of approach r0.
Step by step video & image solution for A projectile of mass m, charge Z', initial speed v and impact parameter b is scattered by a heavy nucleus of charge Z. Use angular momentum and energy conservation to obtain a formula connecting the minimum distance (s) of the projectile form the nucleus to these parameters .show that for b=0, s reduces to the closest distance of approach r_0. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Practice Exercise 1.21videos
ATOMIC PHYSICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Practice Exercise 1.31videos
ATOMIC PHYSICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ATOMIC PHYSICSEXERCISE - Practice Exercise 1.11videos
ATOMIC PHYSICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - CAPACITANCEEXERCISE - UNSOLVED NUMERICAL PROBLEMS40videos
CAPACITANCE
Similar Questions
A particle of mass m, charge q>0 and initial kinetic energy K is projected from infinity towards a heavy nucleus of charge Q assumed to have a fixed position.
(a) If the aim is perfect, how close to the centre of the nucleus is the particle when it comes instantaneously to rest ?
(b) With a particular imperfect aim, the particle's closest approach to nucleus is twicw the distance determined in (a). Determine speed of particle at the closest distance of approach.View SolutionA particle of mass m is moving along the line y=b,z=0 with constnat speed v. State whether the angular momentum of particle about origin is increasing. Decreasing or constant.
View Solution
Knowledge Check
- Question 1 - Select One
When an a-particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze', its distance of closest approach from the nucleus depends on v as:
A1vB1√vC1v2Dv - Question 2 - Select One
When an α particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach form the nucleus depends on m as
A1mB1√mC1m2Dm - Question 3 - Select One
When an α particle of mass m moving with velocity v bombards on a heavy nucleus of charge Ze, its distance of closest approach form the nucleus depends on m as
A1√mB1m2CmD1m
Figure shows a charge +Q clamped at a point in free space. From a large distance another charge particle of charge -q an.d mass m is thrown toward +Q with an impact parameter d as shown with speed v. Find the distance of closest approach of the two particles.
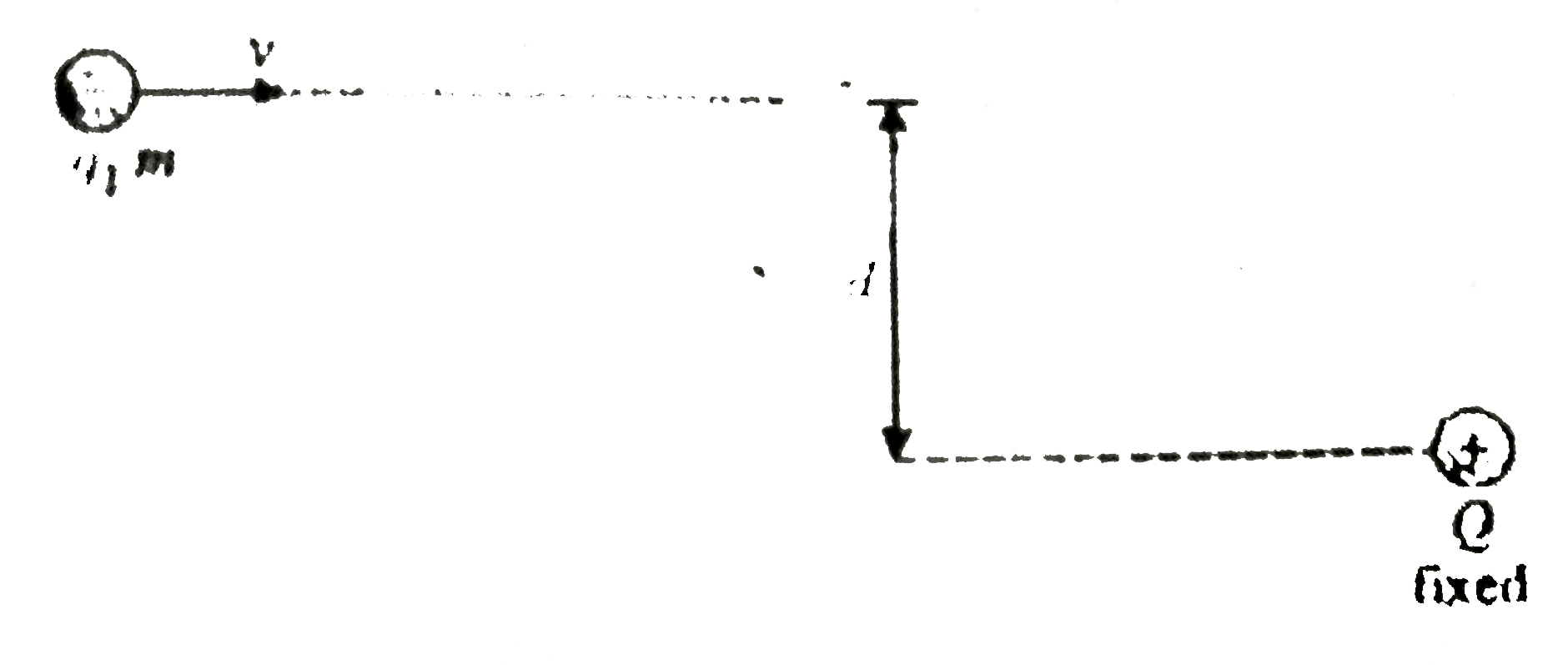 View Solution
View Solutionfor scattering by an inverse square law field (such as that produced by a charged nucleus in Rutherford's model), the relation between impact parameter b and the scattering angle θ is given by
b=Ze2cotθ/24π∈0(12mv2)
(a) What is the scattering angle for b=0?
(b) for given impact parameter, b, does the angle of deflection increase or decrease with increase in energy?
(c) What is the impact parameter at which the scattering angle is 90∘ for Z=79 and initial energy=10MeV?
(d) Why is it that the mass of the nucleus does not enter the formula above, but its charge does?
(e) for a given energy of the projectile, does the scattering angle increase or decrease with decrease in impact parameter?View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
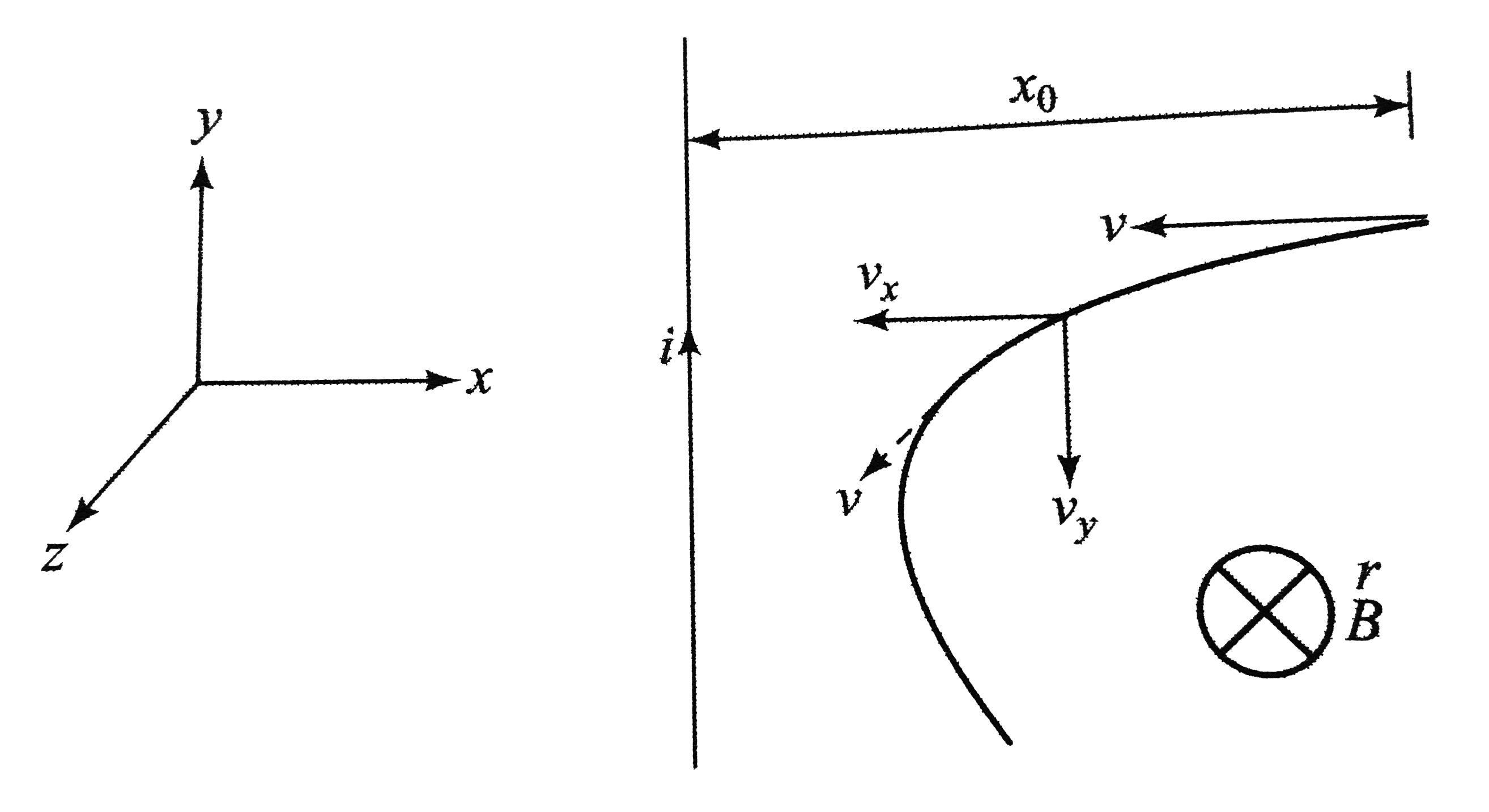
 View Solution
View SolutionWhen an α−particle of mass 'm' moving with velocity 'v' bombards on a heavy nucleus of charge 'Ze' its distance of closest approach from the nucleus depends on m as :
View SolutionIn a Rutherford scattering experiment when a projectile of charge Z1 and mass M1 approaches a target nucleus of charge Z1 and mass M2 , the distance of closest approach is r0 . The energy of the projectile is .
View Solution

