The external diameter of a 5 metre long hollow tube is 10 cm and the thickness of its wall is 5 mm. If the specific resistance of copper be 1.7×105 ohm-metre, then determine its resistance.
To determine the resistance of the hollow tube, we can follow these steps:
Step 1: Identify the given values
- Length of the tube (L) = 5 m
- External diameter = 10 cm = 0.1 m
- Thickness of the wall = 5 mm = 0.005 m
- Specific resistance (resistivity, ρ) of copper = 1.7×10−8 ohm-metre
Step 2: Calculate the internal diameter and radius
- Internal diameter = External diameter - 2 × Thickness
- Internal diameter = 10 cm - 2 × 0.5 cm = 9 cm = 0.09 m
- External radius (R_outer) = External diameter / 2 = 0.1 m / 2 = 0.05 m
- Internal radius (R_inner) = Internal diameter / 2 = 0.09 m / 2 = 0.045 m
Step 3: Calculate the cross-sectional area (A)
The cross-sectional area of the hollow tube can be calculated using the formula:
A=π(R2outer−R2inner)
Calculating the areas:
- R2outer=(0.05)2=0.0025m2
- R2inner=(0.045)2=0.002025m2
Now, substituting these values into the area formula:
A=π(0.0025−0.002025)
A=π(0.000475)
A≈3.14×0.000475≈0.0015m2
Step 4: Calculate the resistance (R)
Using the formula for resistance:
R=ρLA
Substituting the values:
R=1.7×10−8×50.0015
Calculating:
R=8.5×10−80.0015
R≈5.67×10−5ohm
Final Answer
The resistance of the hollow tube is approximately 5.67×10−5 ohms.
---
- Length of the tube (L) = 5 m
- External diameter = 10 cm = 0.1 m
- Thickness of the wall = 5 mm = 0.005 m
- Specific resistance (resistivity, ρ) of copper = 1.7×10−8 ohm-metre
- Internal diameter = External diameter - 2 × Thickness
- Internal diameter = 10 cm - 2 × 0.5 cm = 9 cm = 0.09 m
- External radius (R_outer) = External diameter / 2 = 0.1 m / 2 = 0.05 m
- Internal radius (R_inner) = Internal diameter / 2 = 0.09 m / 2 = 0.045 m
The cross-sectional area of the hollow tube can be calculated using the formula:
A=π(R2outer−R2inner)
- R2outer=(0.05)2=0.0025m2
- R2inner=(0.045)2=0.002025m2
A=π(0.0025−0.002025)
A=π(0.000475)
A≈3.14×0.000475≈0.0015m2
Using the formula for resistance:
R=ρLA
R=1.7×10−8×50.0015
R=8.5×10−80.0015
R≈5.67×10−5ohm
The resistance of the hollow tube is approximately 5.67×10−5 ohms.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems From Competitive
18 Videos
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self
101 Videos
- CHEMICAL EFFECT OF CURRENTBOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B
5 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive
61 Videos
Similar Questions
The external diameter of a 4 m long hollow tube is 10 cm and thickness of its wall is 5 mm. If the specific resistance of the copper is 1.7×10−8Ωm, then calculate its resistance.
View SolutionA hollow copper tube of 5 m length has got external diameter equal to 10 cm and its walls are 5 mm thick. The specific resistance of copper is 1.7×10−8Ω m. The resistance of the copper tube, approximately
View Solution
Knowledge Check
The external diameter of a 314 m long copper tube is 1.2 cm and the internal diameter is 1 cm. calculate its resistance if the specific resistance of copper is 2.2×10−8 ohm-metre.
A2.0×10−1ohmB4.4×10−2ohmC3.14×10−2ohmD2.2×10−2ohmA hollow copper tube of 5 m length has got external diameter equal to 10 cm and the walls are 5 mm thick . If specific resistance of copper is 1.7×10−8 ohm meter. Calculate the resistance of the tube.
A5.77×105ΩB5.77×10−5ΩC5.77×10−7ΩD5.77×107Ω50 turns of a wire of diameter 1mm is wound on a cylinder of radius 5 cm. If the specific resistance of the materical of the wire is 4.5×10−6Ωm, then its resistance is
A9kΩB900ΩC250ΩD90Ω
Length of a hollow tube is 5m, its outer diameter is 10cm and thickness of its wall is 5mm. If resistivity of the material of the tube is 1.7×10−8Ω×m, then resistance of tube will be
View SolutionWhen the resistance of copper wire is 0.1Ω and the radius is 1mm, then the length of the wire is (specific resistance of copper is 3.14×10−8ohm×m)
View SolutionThe dimensions of a block are (1 cm × 1 cm × 100 cm) the specific resistance of its material is 3×10−7 ohm × metre. Then resistance between the rectangular faces is :-
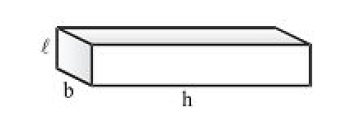
View SolutionDimensions of a block are 1cm×1cm×10cm. If specific resistance of its material is 3×10−7ohm-m, then the resistance between the opposite rectangular faces is
View SolutionDimensions of a block are 1cm×1cm×100cm. If specific resistance of its material is 3×10−7ohm−m, then the resistance between the opposite rectangular facesis
View Solution
