Two identical cells of emf 1.5 V each joined in paralllel provide supply to an external circuit consisting of two resistances of 17Ω each joined in parallel. A very high resistance voltmeter reads the terminal voltage of cells to be 1.4 V. Calculate the internal resistance of each cell.
To solve the problem, we will follow these steps:
Step 1: Identify the given values
- EMF of each cell, E=1.5V
- Terminal voltage, V=1.4V
- Resistance of each resistor, R1=R2=17Ω
Step 2: Calculate the equivalent resistance of the external circuit
Since the two resistances are in parallel, we use the formula for parallel resistances:
Req=R1×R2R1+R2
Substituting the values:
Req=17×1717+17=28934=8.5Ω
Step 3: Calculate the current flowing through the circuit
Using Ohm's law, the current I can be calculated as:
I=VReq=1.48.5≈0.1647A
Step 4: Relate the internal resistance to the terminal voltage
The total internal resistance Rinternal of the two cells in parallel can be expressed as:
V=E−I⋅Rinternal
Rearranging gives:
Rinternal=E−VI
Substituting the known values:
Rinternal=1.5−1.40.1647≈0.10.1647≈0.607Ω
Step 5: Calculate the internal resistance of each cell
Since the internal resistance of two cells in parallel is given by:
Rinternal=R2
where R is the internal resistance of one cell. Thus:
R=2⋅Rinternal=2⋅0.607≈1.214Ω
Final Answer
The internal resistance of each cell is approximately 1.214Ω.
---
- EMF of each cell, E=1.5V
- Terminal voltage, V=1.4V
- Resistance of each resistor, R1=R2=17Ω
Since the two resistances are in parallel, we use the formula for parallel resistances:
Req=R1×R2R1+R2
Substituting the values:
Req=17×1717+17=28934=8.5Ω
Using Ohm's law, the current I can be calculated as:
I=VReq=1.48.5≈0.1647A
The total internal resistance Rinternal of the two cells in parallel can be expressed as:
V=E−I⋅Rinternal
Rearranging gives:
Rinternal=E−VI
Substituting the known values:
Rinternal=1.5−1.40.1647≈0.10.1647≈0.607Ω
Since the internal resistance of two cells in parallel is given by:
Rinternal=R2
where R is the internal resistance of one cell. Thus:
R=2⋅Rinternal=2⋅0.607≈1.214Ω
The internal resistance of each cell is approximately 1.214Ω.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems From Competitive18videos
CURRENT ELECTRICITY
- BOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self101videos
CURRENT ELECTRICITY
- BOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B5videos
CHEMICAL EFFECT OF CURRENT
- BOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive61videos
ELECTRIC POTENTIAL AND ELECTRIC FLUX
Similar Questions
Two identical cells of emf 1.5 V each joined in parallel provided supply to an external circuit cosisting of two resistances of 17Ω each joined in parallel. A very high resistance voltmeter reads. The teminal voltage of cells to be 1.4V. Calculate the internal resistance of each cell.
View SolutionFour identical cells each of emf 2V, are joined in parallel providing supply of current to external circuit consisting of two 15Ω resistors joined in parallel. The terminal voltage of the cells ae read by an ideal voltmeter is 1.6V. Calculate the internal resistance of each cell.
View Solution
Knowledge Check
- Question 1 - Select One
A cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
A2ΩB1.52ΩC1.0ΩD0.5Ω - Question 2 - Select One
Two similar cells, whether joined in series or in parallel, have the same current through an external resistance of 2Ω . The internal resistance of each cell is :
A1ΩB2ΩC0.5ΩD1.5Ω - Question 3 - Select One
If the reading of the ideal voltmeter shown in the circuit is 2V the internal resistance of the two identical cells is
_2019_CBT5_E01_030_Q01.png) A1ΩB0.5ΩC1.5ΩD2Ω
A1ΩB0.5ΩC1.5ΩD2Ω
Two identical cells of emf 1.5V and internal resistance 1Ω are joined in series and the combination is connected in parallel with a third cell of the same emf and internal resistance. Calculalte the terminal voltage of the cells.
View SolutionIn the given circuit, an ideal voltmeter connected across the 10Ω resistance reads 2V. The internal resistance r, of each cell is:
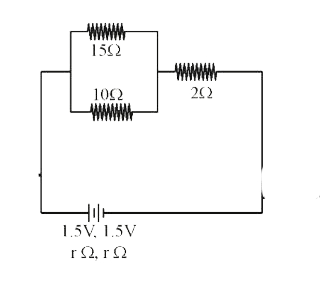 View Solution
View SolutionThree identical cells each of emf 2 V and unknown internal resistance are connected in parallel. This combination is connected to a 5Ω resistor. If the terminal voltage across the cells is 1.5 V, what is the internal resistance of each cell ?
View SolutionThree identical cells each of 2 V and unknow internal resistance are connected in parallel. This combination is connected to a 5 ohm resistor. IF the terminal voltage across the cell is 1.5 volt, what is the internal resistance of each cell?
View SolutionTwo identical cells , whether joined together in series or in parallel give the same current, when connected to external resistance of 1Ω. Find the internal resistance of each cell.
View Solution

