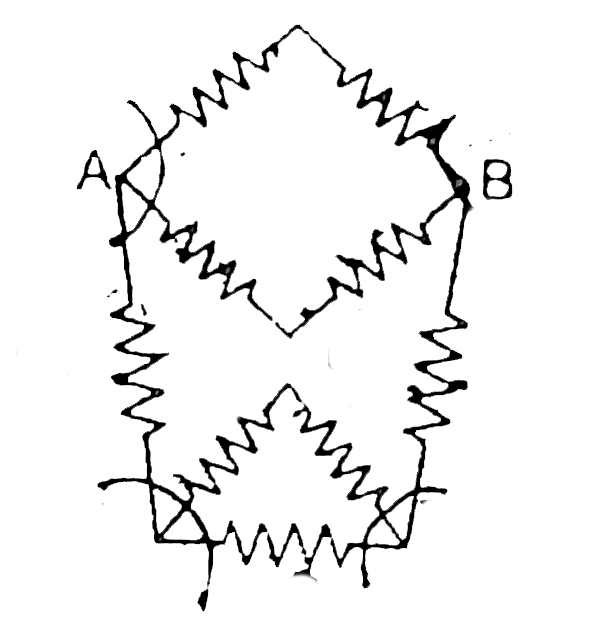Letter A as shown in Fig. 4.57 has resistance on each side of arm. Calculate the total resistance between two ends of the legs.
The correct Answer is:28.75Ω
To calculate the total resistance between the two ends of the legs of the letter A, we will follow these steps:
Step 1: Identify the resistances in series
The letter A has two resistances on the upper part of the letter: one is 10 ohms and the other is 5 ohms. Since these two resistances are in series, we can calculate the equivalent resistance (R1) of this part.
Calculation:
R1=R10+R5=10Ω+5Ω=15Ω
Step 2: Identify the resistances in parallel
Now, we have the equivalent resistance of the upper part (15 ohms) and the resistance on the other leg (5 ohms). These two resistances (15 ohms and 5 ohms) are in parallel.
Calculation:
Using the formula for resistances in parallel:
1Req=1R1+1R2
Where R1=15Ω and R2=5Ω:
1Req=115+15
Finding a common denominator (15):
1Req=115+315=415
Thus,
Req=154Ω=3.75Ω
Step 3: Combine the resistances in series
Next, we need to add the resistance of the lower part of the letter A, which is 10 ohms, to the equivalent resistance we just calculated (3.75 ohms).
Calculation:
Rtotal=Rlower+Req=10Ω+154Ω
Converting 10 ohms to a fraction:
Rtotal=404+154=554Ω=13.75Ω
Final Answer
The total resistance between the two ends of the legs of the letter A is:
Rtotal=554Ω=13.75Ω
---
The letter A has two resistances on the upper part of the letter: one is 10 ohms and the other is 5 ohms. Since these two resistances are in series, we can calculate the equivalent resistance (R1) of this part.
R1=R10+R5=10Ω+5Ω=15Ω
Now, we have the equivalent resistance of the upper part (15 ohms) and the resistance on the other leg (5 ohms). These two resistances (15 ohms and 5 ohms) are in parallel.
Using the formula for resistances in parallel:
1Req=1R1+1R2
Where R1=15Ω and R2=5Ω:
1Req=115+15
Finding a common denominator (15):
1Req=115+315=415
Thus,
Req=154Ω=3.75Ω
Next, we need to add the resistance of the lower part of the letter A, which is 10 ohms, to the equivalent resistance we just calculated (3.75 ohms).
Rtotal=Rlower+Req=10Ω+154Ω
Converting 10 ohms to a fraction:
Rtotal=404+154=554Ω=13.75Ω
The total resistance between the two ends of the legs of the letter A is:
Rtotal=554Ω=13.75Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems From Competitive
18 Videos
- CHEMICAL EFFECT OF CURRENTBOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B
5 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive
61 Videos
Similar Questions
Knowledge Check
In the figure shown, the total resistance between A and B is
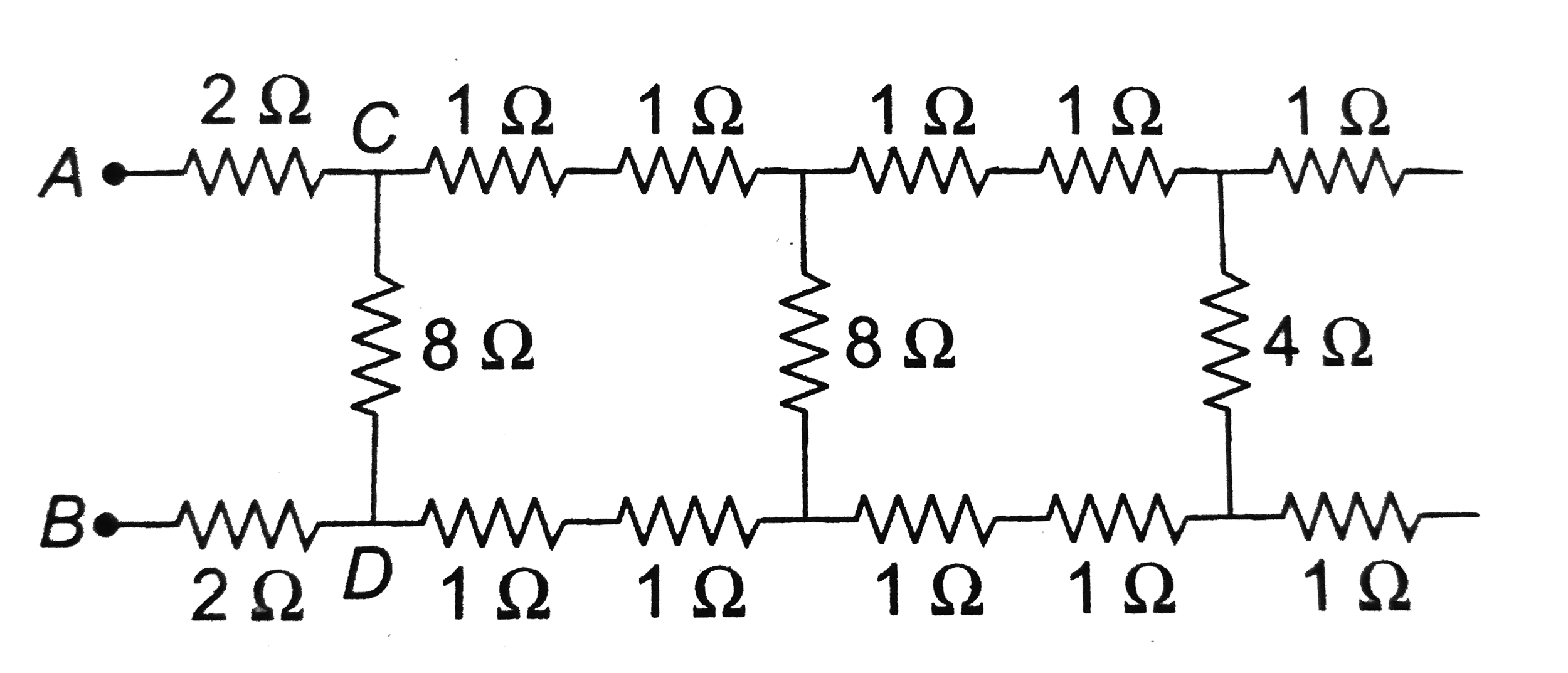 A12ΩB4ΩC6ΩD8Ω
A12ΩB4ΩC6ΩD8ΩIn the figure shown, the total resistance between A and B is
 A50 AB2AC0.5AD109A
A50 AB2AC0.5AD109AEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
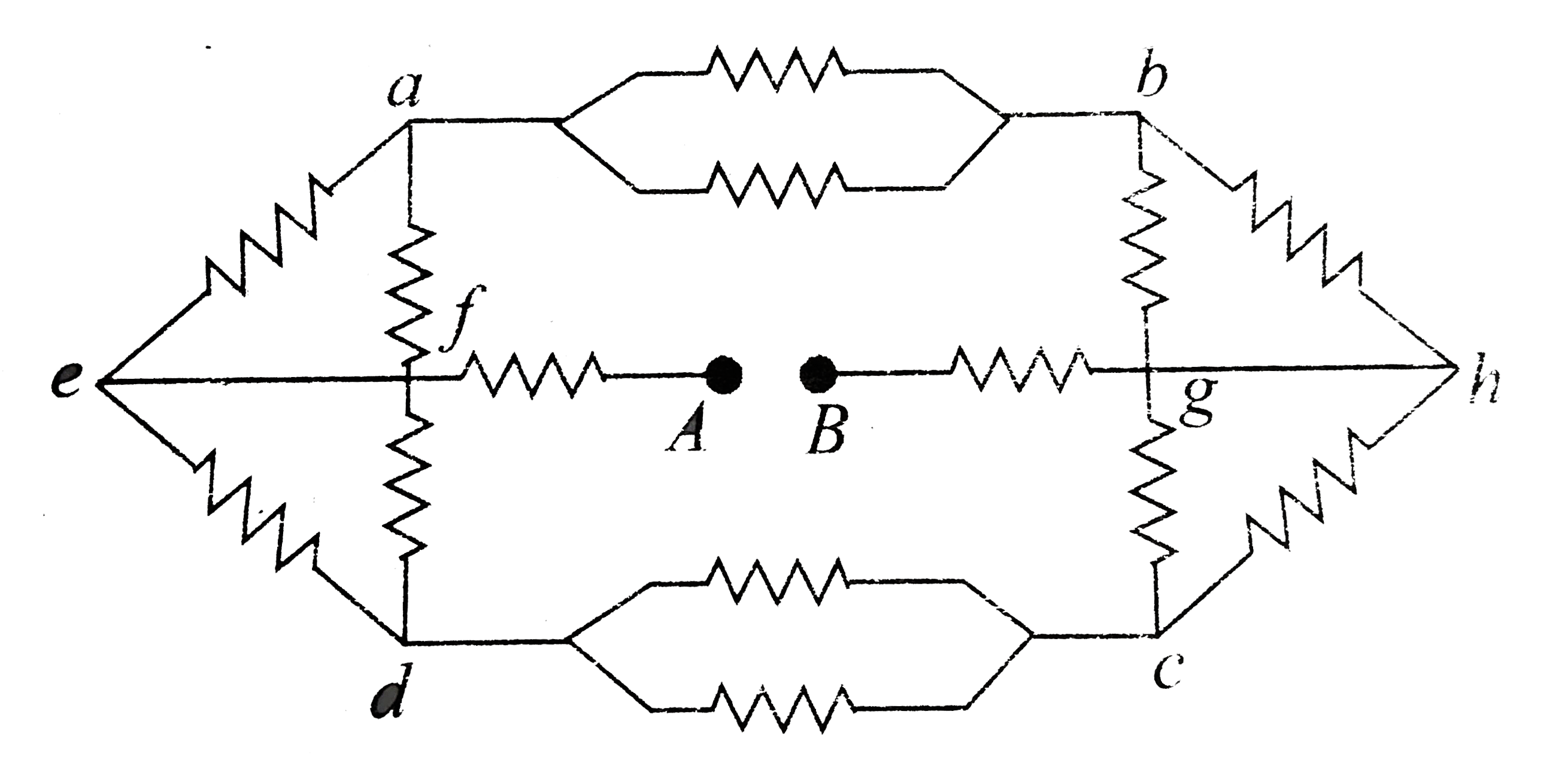 A7R4B5R4C9R4D11R4
A7R4B5R4C9R4D11R4
In the diagram below each resistance is of 1Ω. The total resistance between A and B is
View SolutionCalculate equivalent resistance between A and B of the circuit shown in fig.

View SolutionCalculate effective resistance between A and B if each resistance is R.
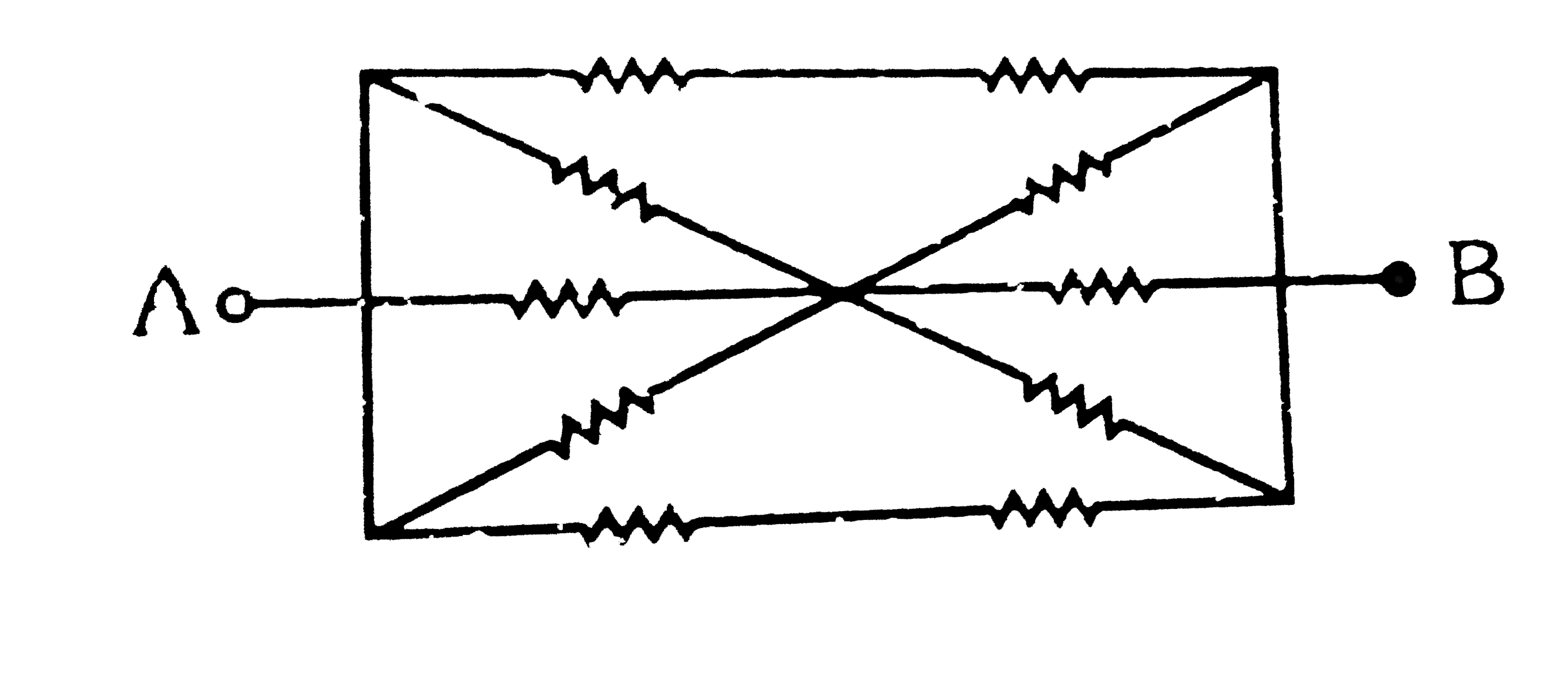
View SolutionEach resistance shown in figure is 2Ω. The equivalent resistance between A and B is
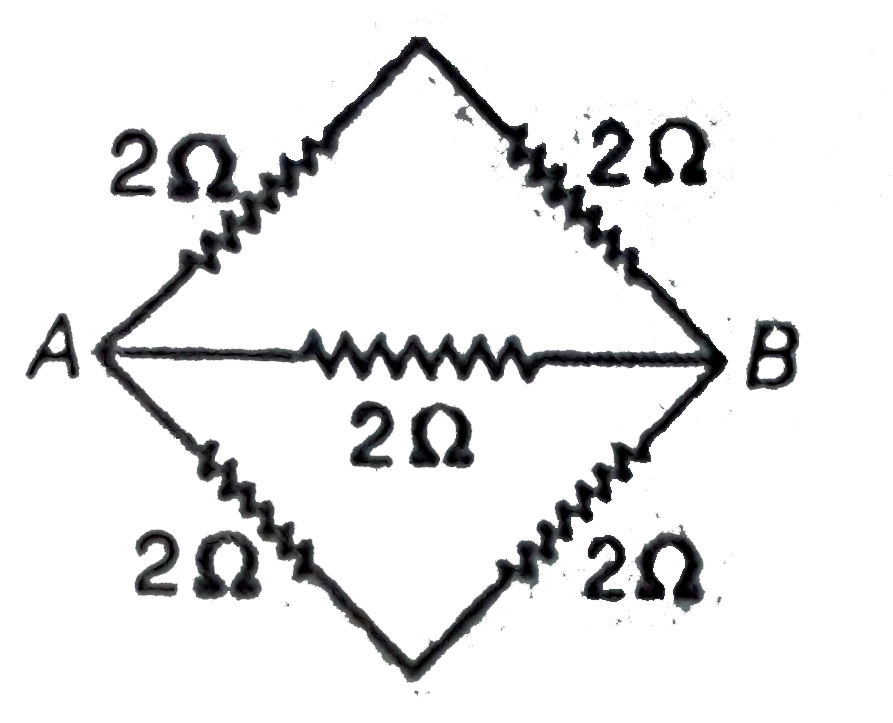
View SolutionEach resistance of the network shown in figure is r. Net resistance between
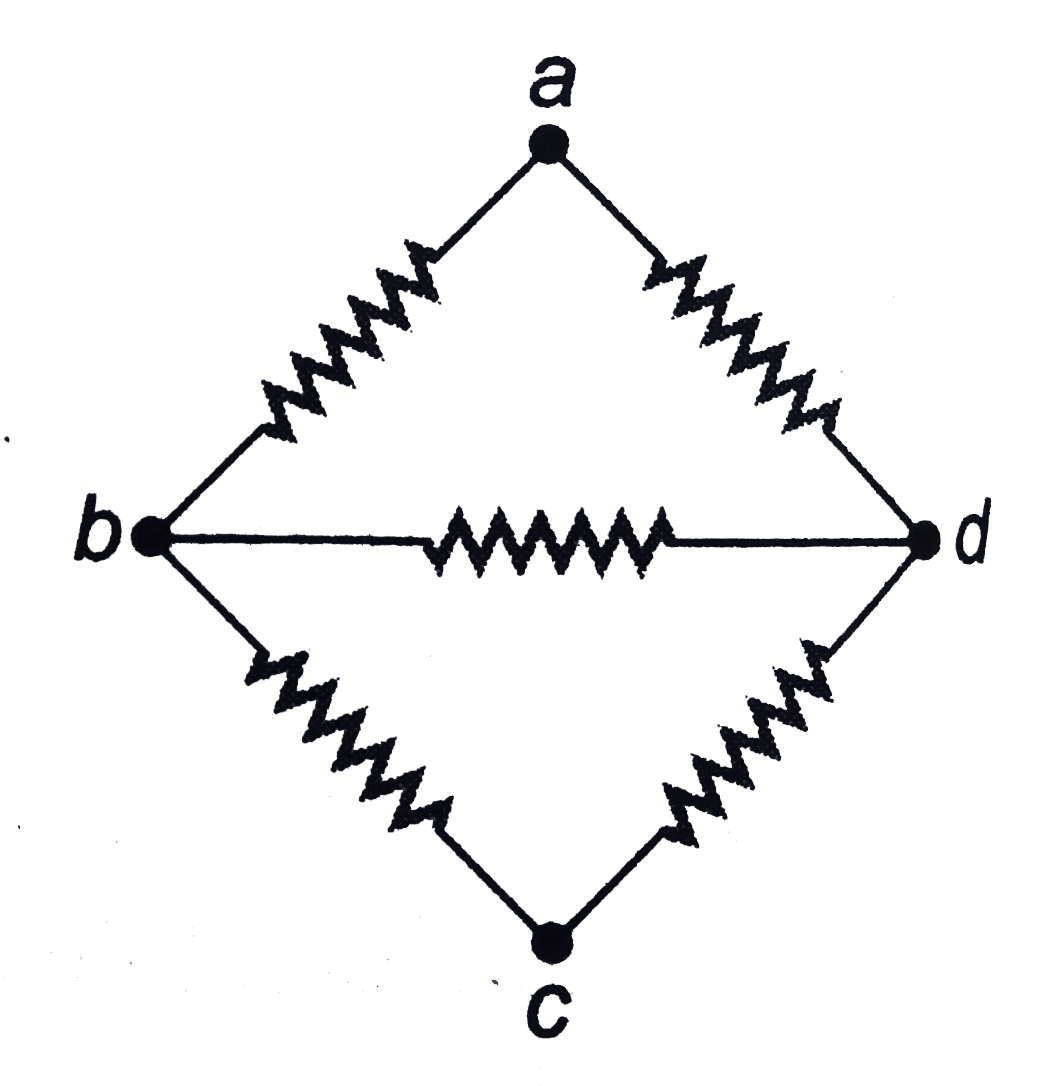
View Solution