A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1'33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface ?
The correct Answer is:At 226 cm from the pole
Step by step video, text & image solution for A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1'33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE F10videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE I12videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE A15videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - OPTICAL INSTRUMENTSEXERCISE - Problems for self practice35videos
OPTICAL INSTRUMENTS
- BOOK - SL ARORACHAPTER - SOLIDS AND SEMICONDUCTOR DEVICESEXERCISE - PROBLEM_TYPE9videos
SOLIDS AND SEMICONDUCTOR DEVICES
Similar Questions
A spherical surface of radius 30cm separates two transparent media A and B with refractive indiecs 1.33 and 1.48 , respectively. The medium A is on the convex side of the surface. Where should a point object the placed in medium A so that the paraxial rays become parallel after refraction at the surface?
View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View Solution
Knowledge Check
- Question 1 - Select One
A concave spherical surface of radius of curvature 10cm separates two mediums X and Y of refractive indices 4/3 and 3/2 respectively. Centre of curvature of the surfaces lies in the medium X. An object is placed in medium X.
AImage is always realBImage is real if the object distance is greater than 90cmCImage is always virtualDImage is virtual only If the object distance is less than 90cm. - Question 2 - Select One
A concave spherical surface of radius of curvature 10 cm separates two medium x & y of refractive index 4/3 & 3/2 respectively. If the object is placed along principal axis in medium X then
 Aimage is always realBimage is real if the object distance is greater than 90cmCimage is always virtualDimage is virtual if the object distance is less than 90 cm
Aimage is always realBimage is real if the object distance is greater than 90cmCimage is always virtualDimage is virtual if the object distance is less than 90 cm - Question 3 - Select One
A spherical convex surface separates object and image space of refractive index 1 and 43 respectively. If radius of curvature of the surface is 0.1 m, its power is
A2.5DB-2.5 DC3.3DD-3.3D
A convex surface of radius of curvature 40 cm separate two media of refractive indices 43 and 1.50. An object is kept in the first medium at a distance of 20 cm from the surface. Calculate the position of the image.
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
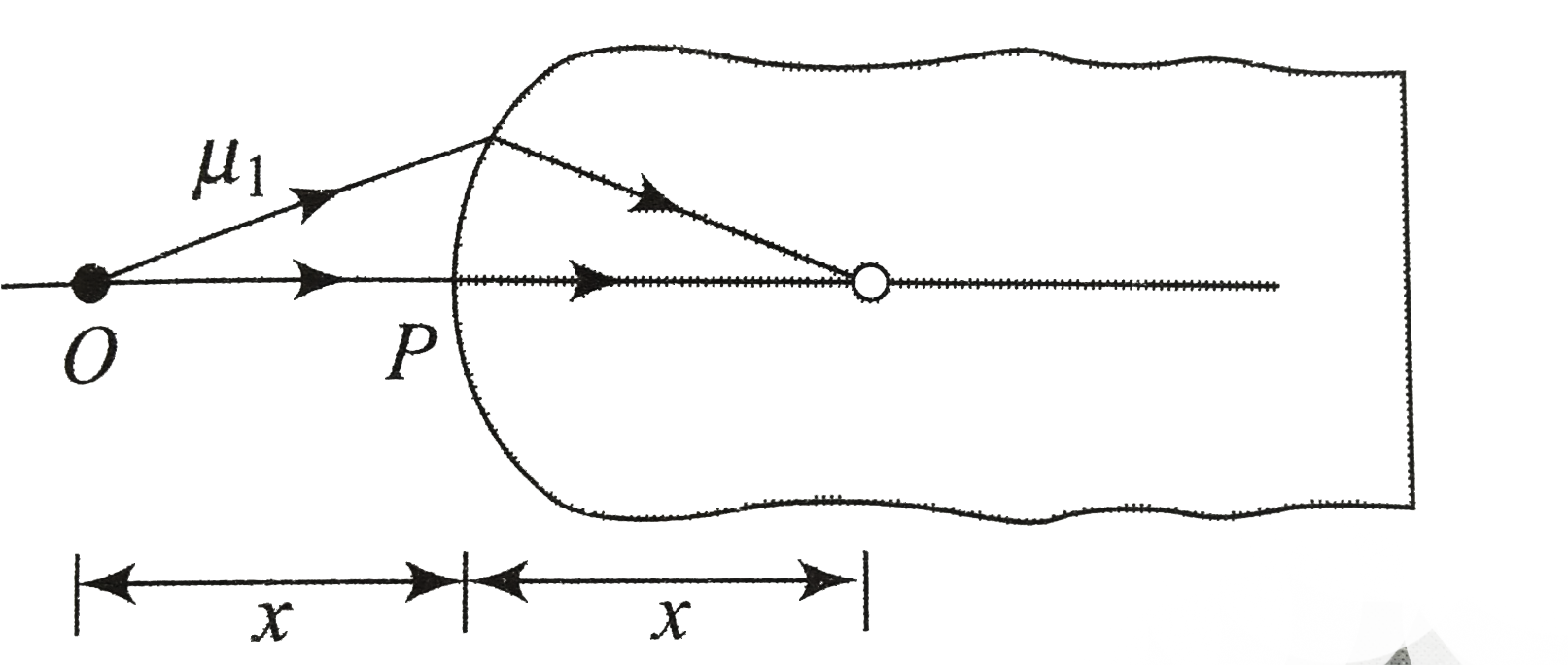 View Solution
View SolutionA concave spherical surface of radius of curvature R=20cm separates two media A and B having refractive indices μA=43 and μB=32respectively. A point object is placed on the principal axis. Find the distance of the object from the surface so that its image is virtual when
(a) the object is in medium A.
(b) the object is in medium B.View SolutionA spherical surface S separates two media 1 and 2 as shown in figure .Find where an object O is placed in medium -I so that the light rays from object after refraction becomes parallel to optic of this system
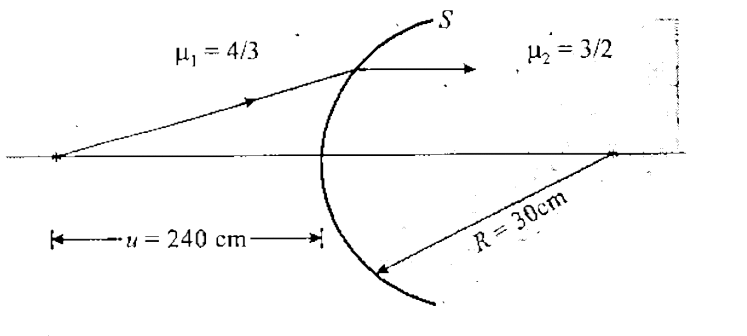
240 cmView SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
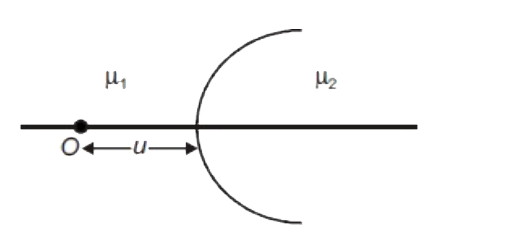 View Solution
View Solution

