If ΔH=mL, where m is mass of body.
ΔH= total thermal energy supplied to the body
L= latent heat of fusion.
Find the dimensions of latent of fusion.
[ML2T−2]
[L2T−2]
[M0L0T−2]
[ML0T−1]
(b) ΔH=mL:[L]=[ML2T−2][M]=[L2T−2]
Topper's Solved these Questions
Similar Questions
Knowledge Check
M g of ice at 0∘C is to be converted to water at 0∘C. If L is the latent heat of fusion of ice, the quantity of heat required for the above operation would be
AML calBMLCLM calDnone of theseOn a cold winter dry, the temperature of atmosphere is −T∘C. The cylindrical dram shown is made of insultating material and it contains water at 0∘C. If L is latent heat of fusion of ice, ρ is density of ice and KR is thermal conductivity of ice, the time taken for total mass of water to freeze is
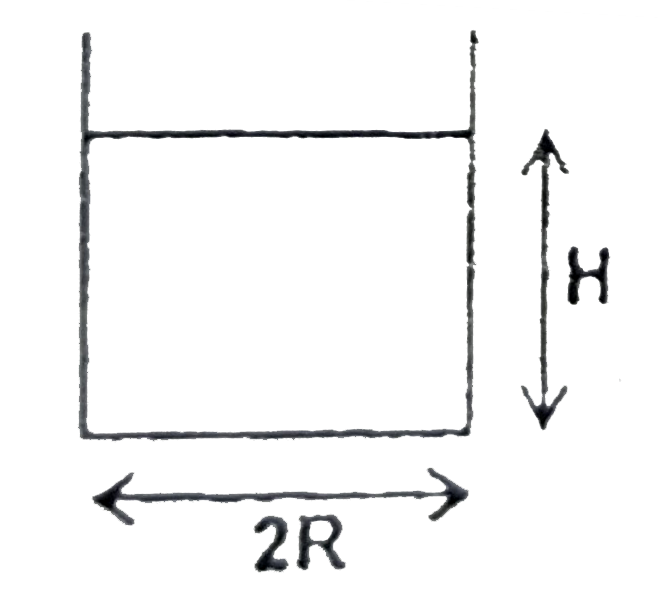 AρLH2KTBρLH22KTCρLH2KTDH2ρLKT
AρLH2KTBρLH22KTCρLH2KTDH2ρLKTA given substance of mass 'm' is in solid state at certain temperature. Arrange the following steps in proper sequence to calculate the total heat energy required to just convert the substance completely into gaseous state.
(A) Note down the specific latent heat of vapor ization of the substance and calculate the heat supplied to convert from liquid to gaseous state using the formula.
(B) Note down the melting point of the substance and calculate the heat supplied to increase the temperature of the solid to its melting point.
(C ) Note down the boiling point of the substance and calculate the heat supplied to increase the temperature of the substance from melting point to its boiling point.
(D) Add all the heat energies, it gives the resultant heat supplied to the solid to just convert it into gaseous state.
(E) Note down the specific latent heat of fusion of the substance and calculate the heat supplied to convert the substance from solid state to liquid state.AB D E C ABA C E D BCA B C D EDB E C A D
A layer of ice of thickness y is on the surface of a lake. The air is at a constant temperature −θ∘C and the ice water interface is at 0∘C. Show that the rate at which the thickness increases is given by
dydt=KθLρy
where, K is the thermal conductivity of the ice, L the latent heat of fusion and ρ is the density of the ice.
View SolutionA layer of ice of thickness y is on the surface of a lake. The air is at a constant temperature −θ∘C and the ice water interface is at 0∘C. Show that the rate at which the thickness increases is given by
dydt=KθLρy
where, K is the thermal conductivity of the ice, L the latent heat of fusion and ρ is the density of the ice.
View SolutionOn a cold winter dry, the temperature of atmosphere is −T∘C. The cylindrical dram shown is made of insultating material and it contains water at 0∘C. If L is latent heat of fusion of ice, ρ is density of ice and KR is thermal conductivity of ice, the time taken for total mass of water to freeze is

View SolutionIs it possible that water evaporates from a spherical drop of water just by means of surface energy supplying the necessary latent heat of vaporisation? The drop does not use its internal thermal energy and does not receive any heat from outside. It is known that water drops of size less than 10–6 m do not exist. Latent heat of vaporisation of water is L=2.3×106Jkg–1 and surface tension is T=0.07Nm–1.
View SolutionA ginven substance of mass 'm' is in solid state at certain temperature. Arrange the following steps in proper sequence to calcualte the total heat energy required to just convert the substance completely into gaseous state.
(a). Note down the specific latent heat of vaporization of the substance and calculate the heat supplied to convert from liquid to gaseous state using the formula.
(b) Note down the melting point of the substance and calculate the heat supplied to increase the temperature of the solid to its melting point.
(c) Note down the boiling point of the substance and calculate the heat supplied to increase the temperature of the substance from melting point to its boiling point.
(d). Add all the heat energies, it gives the resultant hea supplied to the solid to just convert it into gaseous state.
(e) Note down the specific latent heat of fusion of the substance and calculate the heat supplied to convert the substance from solid state to liquid state.
View Solution
