The expression for drift speed is vd=Jne
Here J= current density,
n= number of electrons per unit volume,
e=1.6×10−19 unit
The unit and dimension of e are
coulomb and [AT]
ampere per second aned [AT−1]
No sufficient information
None of the above
(a) ∵vd=Jne
[e]=[Jnvd]=[AL−2][1L3][LT−1]=[AT]= amp-second= coulomb
Topper's Solved these Questions
Similar Questions
Show that drift velocity of electrons in a conductor is given by u = J≠ where J is the current density, n is the number of mobile electrons per unit volume and e is the charge carried by each electron. Calculate the same in a copper wire of radius of 0.6mm when a current of 1A flows through it assuming that one mobile electron is available from one atom of copper. Atomic weight of copper = 63.55, density of copper = 8930 kgm^(-3),Avogadroνmber=6.01 xx 10^(26)Kgmol^(-1)ande=1.6 xx 10^(-19)C
View SolutionCalculate the drift speed developed in a metal wire when V potential difference is applied across length l of the wire. The number of free electrons per unit volume is n and conductivity of the material is σ.
View Solution
Knowledge Check
If A is the area of cross section of conductor, e be the charge on the electrons, n be the number of electrons per unit volume and J be the current density then drift velocity of electrons is
Avd=Jn eBvd=J⋅neCvd=ne/JDvd=J2neIf A is the area of cross section of conductor, vd is the drift velocity of electrons and n is the number of electrons per unit volume, then current density through conductor is
Ane vdBneAvdCnevdAD(na)AvdA piece of n-type semiconductor is sunjected to an electric E. The left end of the semiconductor is exposed to a radiation so that electron-hole pairs are generated continuously. Let n be the number density of electron. The electron current density Je is given Je=enμeEx+eDedndx . The dimensions of electron drift mobility (μe) . and electron diffusion coefficient (De) are respectively
A[M−1T2]and[L2T1]B[M1T2I−1]and[M1L2T1]C[M−1T2I1]and[L2T1]D[M−1T2I2]and[L1T−2I1]
A small but measurable current of 1.2×10−10A exists in a copper wire whose diameter is 3.0 mm. The number of charge carriers per unit volume is 8.49×1028m−3m. Assuming the current is uniform, calculate the (a) current density and (b) electron drift speed.
View SolutionA current I is passed through a silver strip of width d and area of cross-section A. The number of free electrons per unit volume is n
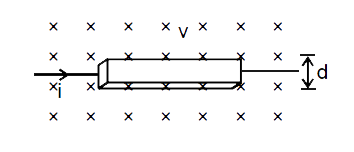
Find the drift velocity v of the electrons.
View SolutionThe charges on an object is given by Q = ne, here n is number of electrons and e is electronic charge (−1.6×10−19C). If an object has charge −5×10−19C, what should be number of excess electron on it?
View SolutionCalculate the relaxation time and mean free path at room temperature (i.e. 27∘C). If the number of free electrons per unit volume is 8.5×1028/m3 and resistivity ρ=1.7×108Ω−m. Given that mass of electron =9.1×10−31kg
e=1.6×10−19Candk=1.36×10−23JK−1
View SolutionA long solenoid with 40 turns per cm carries a current of 1 A. The magnetic energy stored per unit volume is..... J m−3.
View Solution
