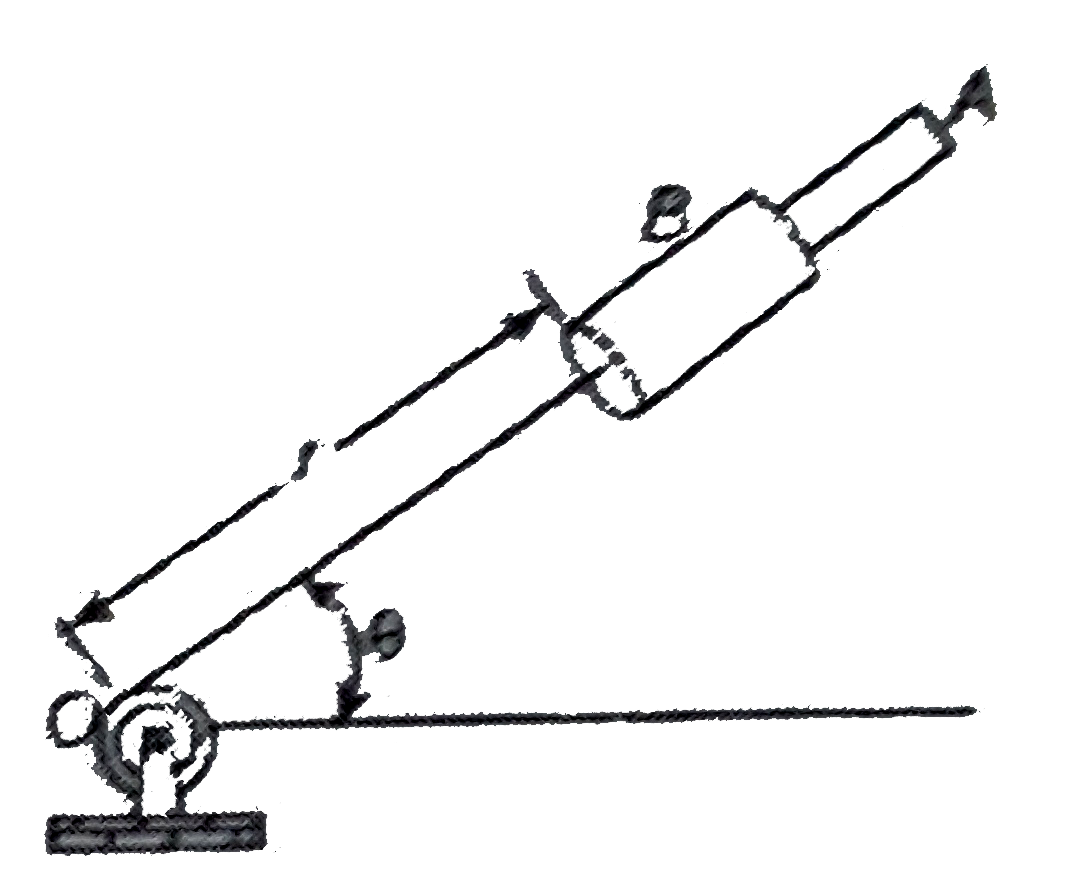
The angular displacement of the rod is defied a s $0 = \frac{3}{20} t^{2}$ where $θ$ is in radian and t is in second. The collar B slides along the rod in such a way that its distance from O is $r = 0.9 - 0.12 t^{2}$ where r is in metre and t is secnd The velocity of collar at $θ = 30^{\circ}$ is

$0.45 m / s$

$0.48 m / s$

$0.52 m / s$

$0.27 m / s$

Video Solution

Text Solution

Verified by Experts

(c) $∴ v_{r} = \frac{D r}{d t} = - 024 t$
$v_{1} r ω = r \frac{d θ}{d t} = r (\frac{6}{20} t) = (0.9 - 0.12 t^{2}) (\frac{6 t}{20})$
$∴ v = (\sqrt{v_{r}^{2} + v_{t^{2}}^{2}}$
$∴ θ = \frac{3}{20} t^{2} or \frac{π}{6} = \frac{3}{20} t^{2}$
$∴ t = \sqrt{(\frac{20 π}{18})}$
Putting the value of $θ, v = 0.25 m / s$

Updated on:21/07/2023