Find the molar specific heat of mixture at constnat volume. It one mole of a monoatomic gas is mixed with three moles of a diatomic gas.
3.33R
225R
115R
6.72R
Step by step video & image solution for Find the molar specific heat of mixture at constnat volume. It one mole of a monoatomic gas is mixed with three moles of a diatomic gas. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - BITSAT GUIDECHAPTER - LAWS OF THERMODYNAMICSEXERCISE - 28
1 Videos
- LAWS OF THERMODYNAMICSBOOK - BITSAT GUIDECHAPTER - LAWS OF THERMODYNAMICSEXERCISE - 29
1 Videos
- LAWS OF THERMODYNAMICSBOOK - BITSAT GUIDECHAPTER - LAWS OF THERMODYNAMICSEXERCISE - 26
1 Videos
- HEAT, TEMPERATURE AND CALORIMETRYBOOK - BITSAT GUIDECHAPTER - HEAT, TEMPERATURE AND CALORIMETRYEXERCISE - Bitsat archives
9 Videos
- MAGNETOSTATICS BOOK - BITSAT GUIDECHAPTER - MAGNETOSTATICS EXERCISE - BITSAT Archives
8 Videos
Similar Questions
Knowledge Check
Graph for specific heat at constant volume for a monoatomic gas
A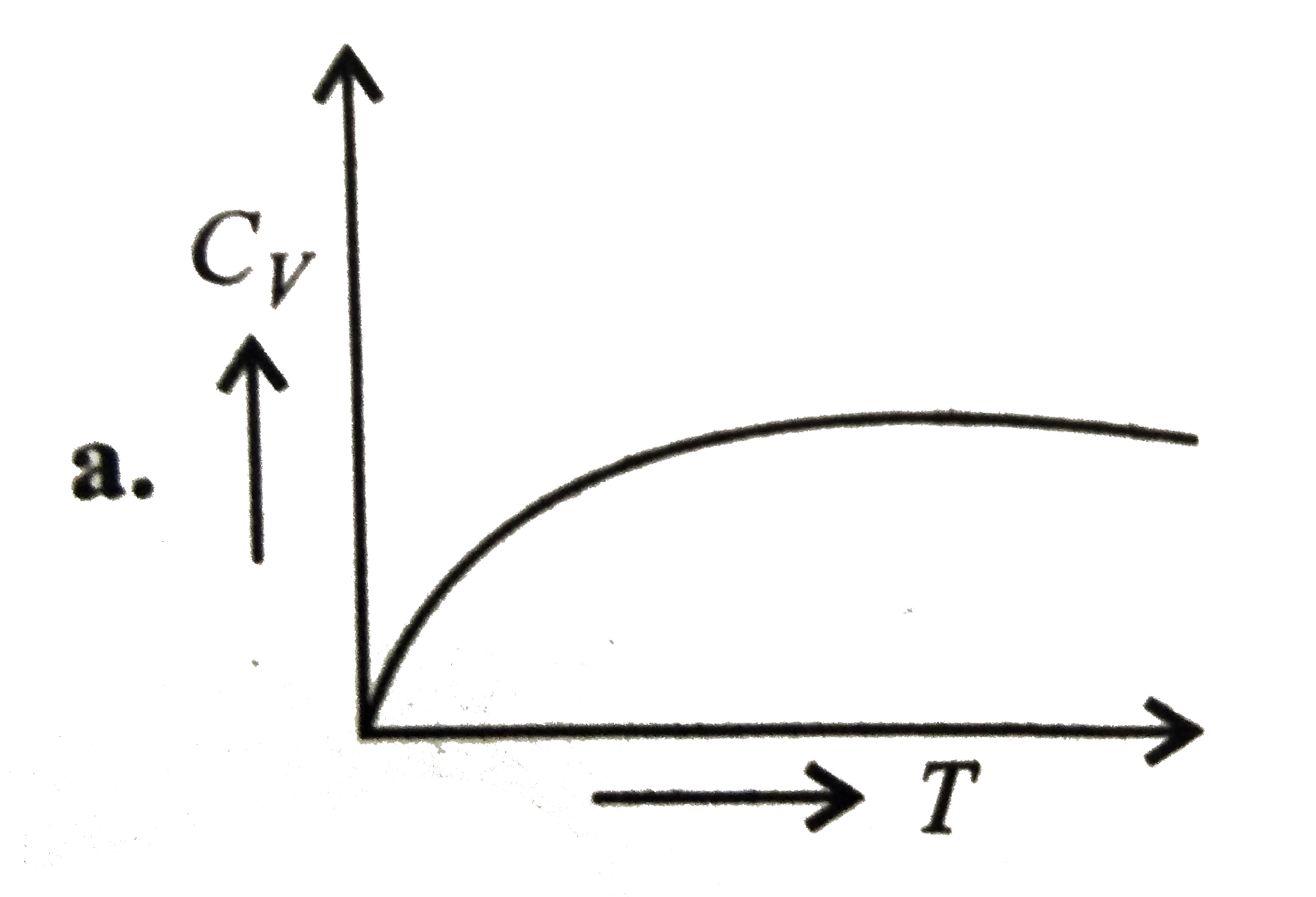 B
B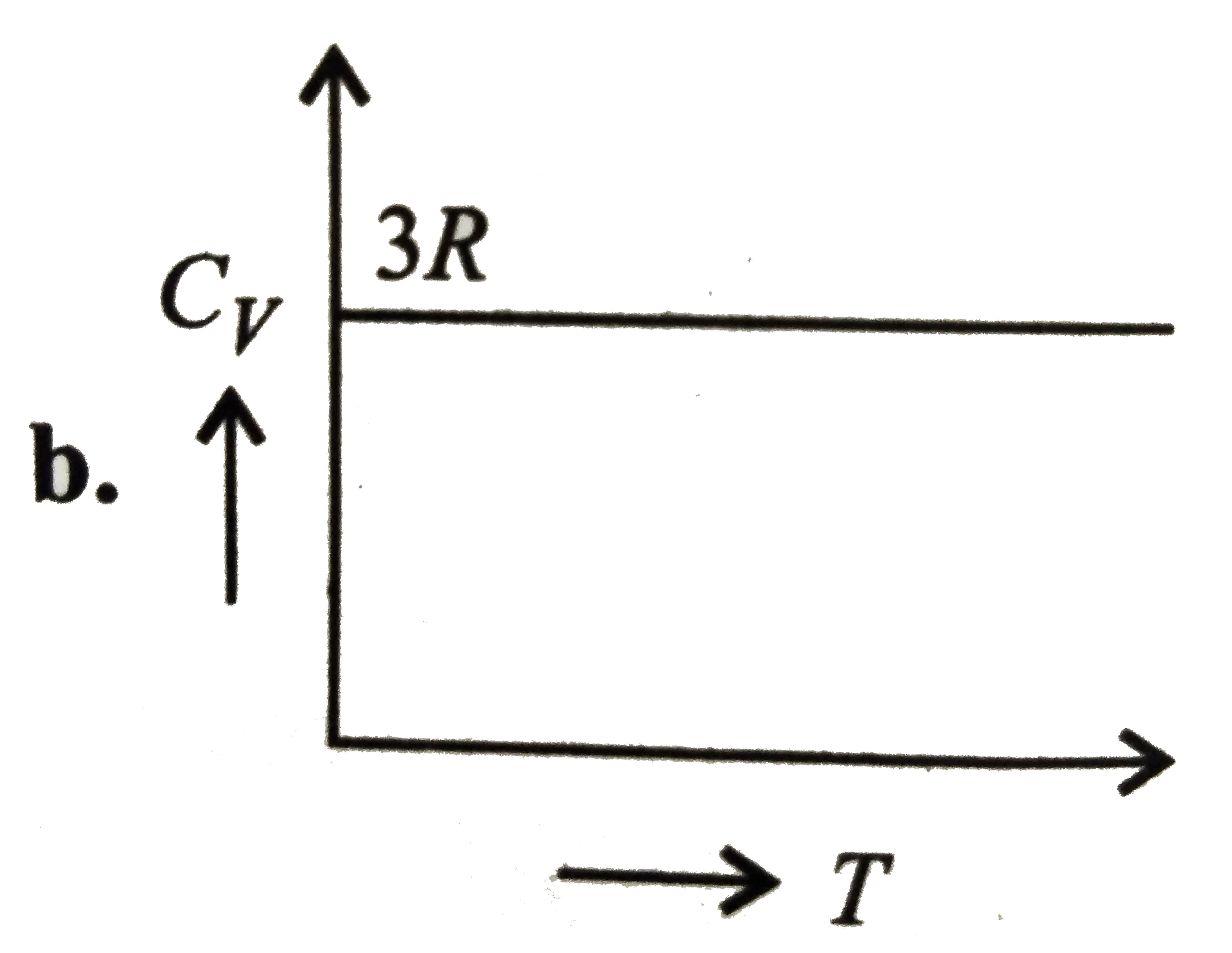 C
C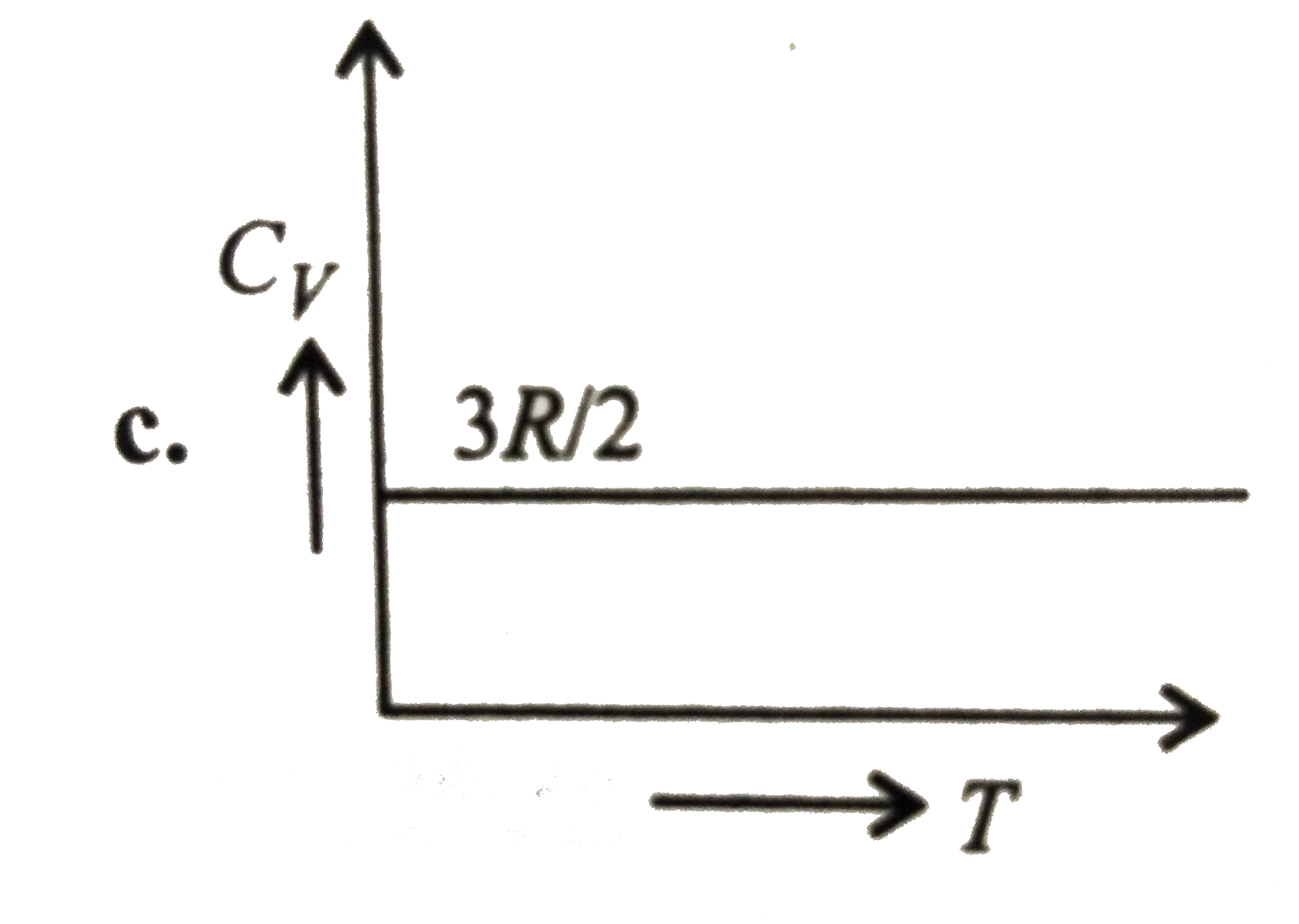 D
DFor one mole of a diatomic gas γ is equal to
A35B53C75D86Graph for specific heat at constant volume for a monoatomic gas
A B
B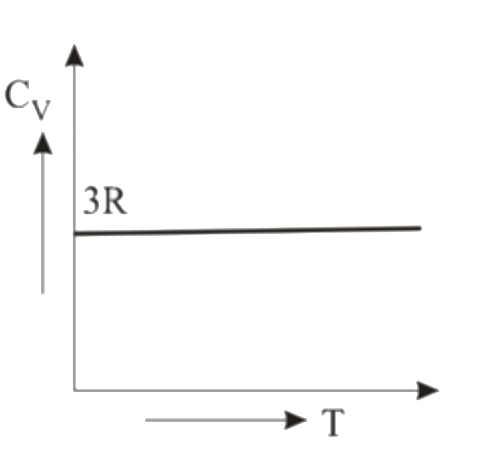 C
C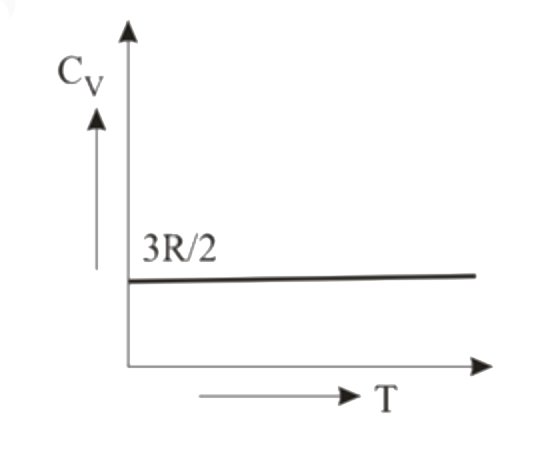 D
D
The molar specific heat at constant pressure of monoatomic gas is
View SolutionOne mole of a monoatomic gas is mixed with 3 moles of a heat of the mixture at constant volume ? Take R=8.31jmole/K.
For monoatomic gas, Cv=3R/2 and for diatommic gas, Cp=5R/2.
View SolutionA mixture of n1 moles of monoatomic gas and n2 moles of diatomic gas has γ=1.5
View SolutionCalculate the average molar heat capacity at constant volume of a mixture containing 2 moles of monoatomic and 3 moles of diatomic ideal gas.
View SolutionAssertion: Molar specific heat at constant volume of an ideal diatomic gas is [32R+R].
Reason: On heating 1 mole an ideal diatomic gas at constant pressure of 1∘C rise in temperature, the increase in internal energy of gas is 72R.
View Solution