Question

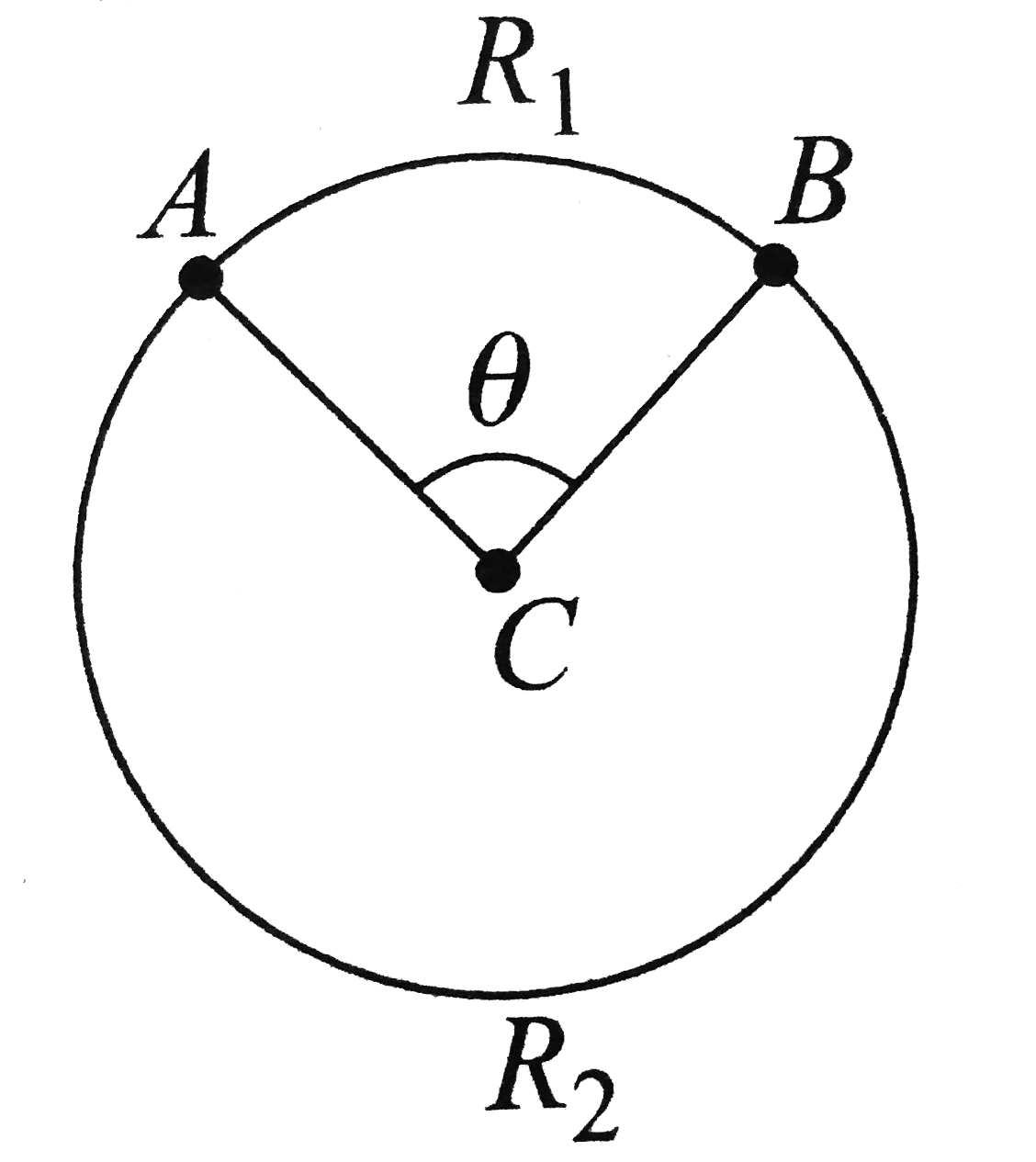
A uniform metal ring with centre $C$ have two points $A$ and $B$ such that angle $ACB$ is $\theta$. $A$ and $B$ are maintained at two different constant temperature.
If the angle between $A$ and $B$ i.e. $\theta ={180}^{\circ }$ the rate of heat flow from $A$ and$B$ is $1.2W$, then what will be the rate, when $\theta ={90}^{\circ }$?

Options

A. `0.6W`
B. `0.9W`
C. `1.6W`
D. `1.8W`

Explanation

To solve the problem, we need to analyze the heat flow through a uniform metal ring when the angle between two points A and B changes. We will use the principles of thermal resistance and heat flow.

1. Understanding the Setup:
- We have a uniform metal ring with center C.
- Points A and B are on the ring, and the angle ACB is denoted as θ.
- We know that when θ = 180°, the rate of heat flow (Q1) is 1.2 W.

2. Heat Flow Formula:
- The rate of heat flow through a conductor is given by the formula:
\( Q = \frac{\Delta T}{R} \)
- Where Q is the heat flow rate, ΔT is the temperature difference, and R is the thermal resistance.

3. Case 1: θ = 180°:
- When θ = 180°, the points A and B are at opposite ends of the ring.
- The total resistance of the ring can be considered as two halves in series:
\( R_{eq1} = R/2 + R/2 = R \)
- Thus, we can write:
\( Q_1 = \frac{\Delta T}{R} \)
- Given that \( Q_1 = 1.2 \, \text{W} \):
\( 1.2 = \frac{\Delta T}{R} \)

4. Case 2: θ = 90°:
- When θ = 90°, points A and B are at a quarter of the circumference apart.
- The equivalent resistance for this configuration can be calculated as follows:
- Each segment of the ring contributes a resistance of \( R/4 \).
- The total resistance for two segments in parallel is:
\( R_{eq2} = \frac{R/4 \cdot R/4}{R/4 + R/4} = \frac{R^2/16}{R/2} = \frac{R}{8} \)

5. Calculating Heat Flow for θ = 90°:
- Using the heat flow formula for θ = 90°:
\( Q_2 = \frac{\Delta T}{R_{eq2}} = \frac{\Delta T}{R/8} = \frac{8\Delta T}{R} \)

6. Relating Q2 to Q1:
- From the first case, we have \( \Delta T = 1.2R \).
- Substituting this into the equation for Q2:
\( Q_2 = \frac{8 \cdot (1.2R)}{R} = 9.6 \, \text{W} \)

7. Final Result:
- Therefore, the rate of heat flow when θ = 90° is:
\( Q_2 = 9.6 \, \text{W} \)