The least value of n for which 1+2+22+... to n terms is greater than 1000 is
Video Solution
|
Answer
Step by step video & image solution for The least value of n for which 1+2+2^2 +... to n terms is greater than 1000 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Find the least value of n for which th sum 1+2+22+… to n terms is greater than 3000.
A8B10C12D1522^n+1 where n is positive integer greater than one ends is
A5B7C9Dany number
If n=(√2+1)6. Then the integer just greater than n is
View SolutionFind the least value of n for which 1+3+32+…3n−1>1000
View SolutionFind the least value of n for which 1+3+32+........+3n−1>1000
View SolutionIn the expansion of (51/2+71/8)1024 if the number of integral terms is N3, then the integer just greater than N is
View Solution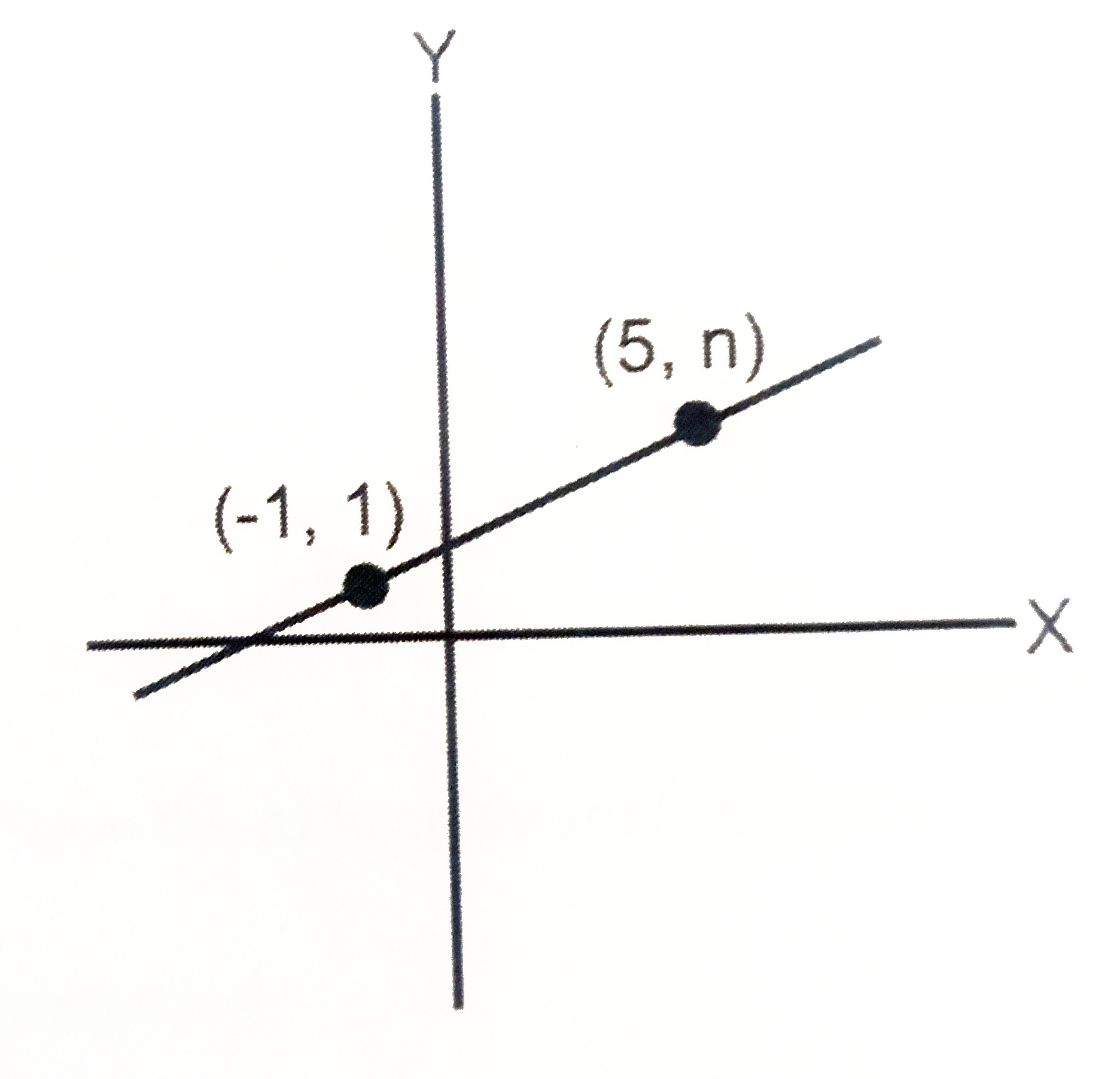
The graph above depicts a straight line passing through (-1, 1) and (5, n). What is the least integer value of n if the slope is greater than 23 ?
View SolutionIf Sn=1+12+122+….+12n−1, find the least value of n for which 2−Sn<1100.
View Solution
