In a circle with center O, the measure of central angle POQ is 3π2 radians. The length of the arc formed by central angle POQ is that fraction of the circumference of the circle?
316
38
34
32
The correct Answer is:C
To solve the problem, we need to find the fraction of the circumference of the circle that corresponds to the length of the arc formed by the central angle POQ, which measures 3π2 radians.
1. Identify the Circumference of the Circle:
The formula for the circumference C of a circle with radius r is given by:
C=2πr
2. Determine the Length of the Arc:
The length L of the arc corresponding to a central angle θ (in radians) can be calculated using the formula:
L=rθ
Here, the central angle θ is given as 3π2. Therefore, the length of the arc L becomes:
L=r⋅3π2=3πr2
3. Calculate the Fraction of the Circumference:
To find the fraction of the circumference that the arc length represents, we take the ratio of the arc length L to the circumference C:
Fraction=LC=3πr22πr
4. Simplify the Fraction:
In the fraction, we can cancel πr from the numerator and the denominator:
Fraction=322=32⋅12=34
5. Conclusion:
Thus, the length of the arc formed by the central angle POQ is 34 of the circumference of the circle.
Final Answer:
The length of the arc formed by central angle POQ is 34 of the circumference of the circle.
---
The formula for the circumference C of a circle with radius r is given by:
C=2πr
The length L of the arc corresponding to a central angle θ (in radians) can be calculated using the formula:
L=rθ
Here, the central angle θ is given as 3π2. Therefore, the length of the arc L becomes:
L=r⋅3π2=3πr2
To find the fraction of the circumference that the arc length represents, we take the ratio of the arc length L to the circumference C:
Fraction=LC=3πr22πr
In the fraction, we can cancel πr from the numerator and the denominator:
Fraction=322=32⋅12=34
Thus, the length of the arc formed by the central angle POQ is 34 of the circumference of the circle.
The length of the arc formed by central angle POQ is 34 of the circumference of the circle.
Topper's Solved these Questions
- BOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 14: FUNCTIONS11videos
PROBLEM SETS
- BOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 15: GRID-INS11videos
PROBLEM SETS
- BOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 12: CIRCLES, QUADRILATERALS, AND VOLUME11videos
PROBLEM SETS
- BOOK - PRINCETONCHAPTER - PRACTICE TEST 4EXERCISE - Math Test-Calculator38videos
PRACTICE TEST 4
- BOOK - PRINCETONCHAPTER - SAT MATH: THE BIG PICTUREEXERCISE - Example4videos
SAT MATH: THE BIG PICTURE
Similar Questions
In a circle with center O, central angle AOB has a measure of 5π4 radians. The area of the sector formed by central angle AOB is what fraction of the area of the circle?
View Solution
Point O is the center of the circle above. What fraction of the circumference of the circle is the length of the bolded arc?View Solution
Knowledge Check
- Question 1 - Select One

In the xy-plane above, the circle has center O, and the measure of ∠XOY is πn radians. What is the value of n?A1B3C6D12 - Question 2 - Select One
Point X and Y lie on a circle with center C such that the measure of the minor are formed by central angle XCY is 310 of the circumference of the circle. What is the measure of angle XYC, in radians?
A310πB35πC65πD53π - Question 3 - Select One
A central anglej of two concentric circles is 3π14. The area of the large sector. What is the ratio of the lengths of the radii of the two circles?
A0.25:1B0.50:1C0.67:1D0.71:1
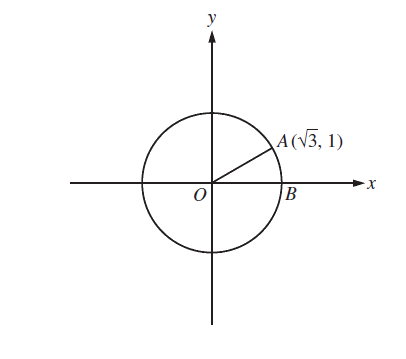
In the xy-plane above, O is the center of the circle, and the measure of ∠AOB is πa radians. What is the value of a ?View SolutionThe radius of a circle is 3.6 cm. Find the length of the arc of the sector with central angle 36∘
View SolutionIf an arc forms 72∘ at the centre of the circle. Find the ratio of its length to circumference of circle.
View Solution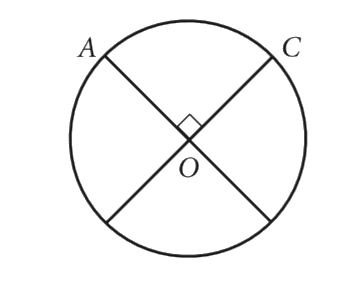
The circle above with center O has a circumference of 36. What is the length of minor arc AB⌢View Solution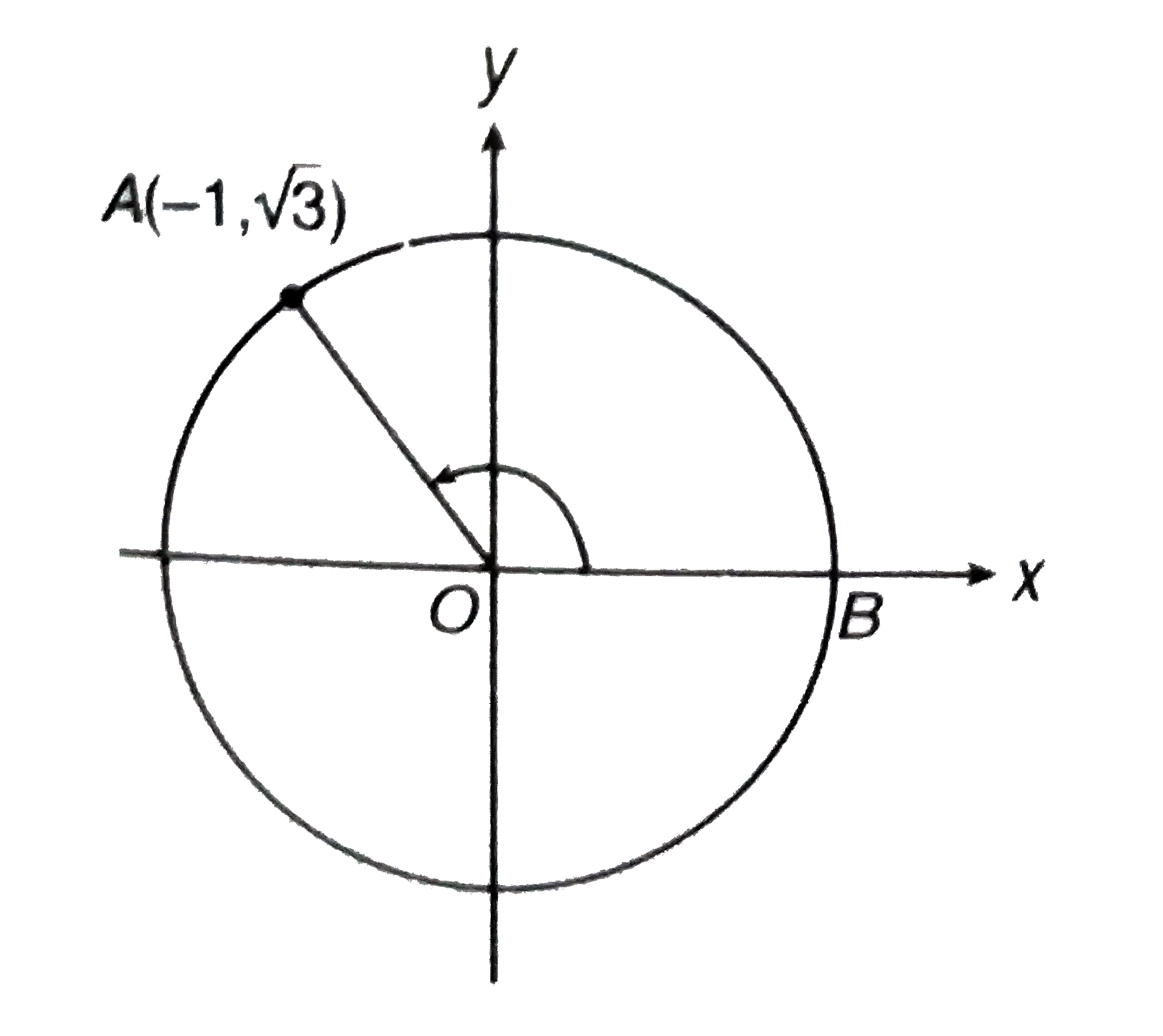
In the xy-plane above, O is the center of the circle, and the measure of ∠AOB is kπradians. What is a possible value for k?View Solution

