At any instant, a rolling body may be considered to be in pure rotation about an axis through the point of contact. This axis is translating forward with speed
equal to centre of mass
zero
twice of centre of mass
None of these
The correct Answer is:A
Since, in this case instantaneous axis of rotation is always below the centre of mass. This is possible only when point of contact moves with a velocity equal to centre of mass.
Topper's Solved these Questions
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(A) Chapter Exercises
Explore 83 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(B) Chapter Exercises
Explore 25 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:Check point 9.2
Explore 20 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Integer type q.
Explore 15 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Subjective Questions
Explore 2 Videos
Similar Questions
a) show that the energy of a rolling body which is not slipping is equivalent to that of pure rotatioin with the same angular speed about an axis through the point of contact of the rolling body.
b) Show that the angular momentum of a body of mass M which is rolling without slippint about any point is equal to its angular momentum about its center plus the moment of momentum of a particle of the same mass M concentrated at its center and moving with the speed of the center of the mass of the body about the same point
View SolutionThe axis of rotation of a purely rotating body
View Solution
Knowledge Check
For a rotating body about fixed axis ,
Aevery particle moves in a circleBthe linearvelocity is related to angular velocityCBoth (1) and (2) are correctDBoth (1) and (2) are incorrectA rigid body is rotating about an axis. The best way to stop it is applying
Apressure at the turning point.Bupward force at the turning point.Cdownward force at the free end.Dtorque in opposite direction.In the above problem the moment of inertia of four bodies about an axis passing through any side of frame is
A4ML2B2√2ML2C2ML2D√2ML2
Consider three bodies : a ring, a disc and a sphere. All the bodies have same mass and radius. All rotate about their axis through their respective centre of mass and perpendicular to the plane. What is the ratio of moment of inertia ?
View Solutionif rod is rotated about an axis passing through its mid-point , the potential difference between the ends of rod is
View SolutionA rigid body of mass m rotates with angular velocity ω about an axis at a distance a from the centre of mass G. The radius of gyration about a parallel axis through G is k. The kinetic energy of rotation of the body is
View SolutionIf the speed of rotation of earth about its axis is increased,
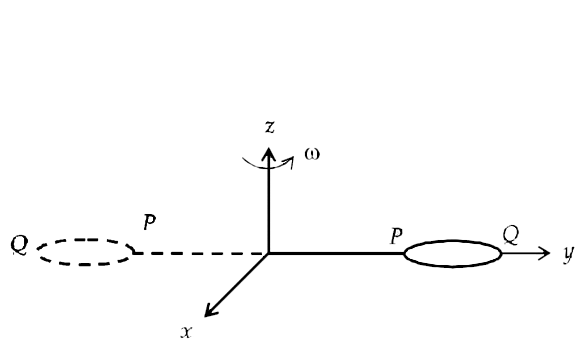
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
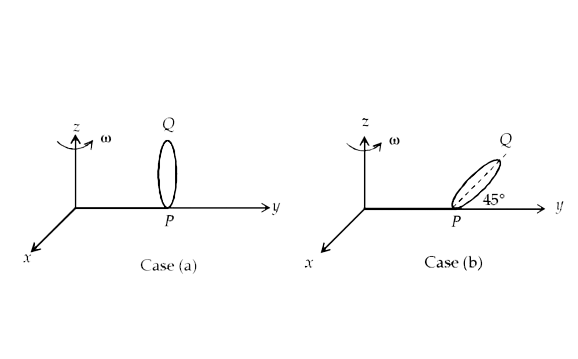
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View Solution