Three rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

Total thermal resistance
R=R1+R2+R93)=(L1K1A)+L2K2A+L3K3A
Now, Heat transfer H=T1−T2R
∴ H=T1−T2L1K1A+L2K2A+L3K3A
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.110videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.210videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective14videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
Similar Questions
A rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionConsider two rods of equal cross - sectionai area A, one of Aluminium and other of iron joined end to end as shown in figure -4.8. Length of the two rods and their thermal coductivities are l1,k1and l2,k2 respectively . If the ends of the rods are maintained at temperature T1 and T2,(T1>T2) find the temperature of the junction in steady state .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
AdQdt=KL(T1−T2)ABdQdt=KL(T1−T2)LACdQdt=KLA(T1−T2)DdQdt=KA(T1−T2)L - Question 2 - Select One
Three rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
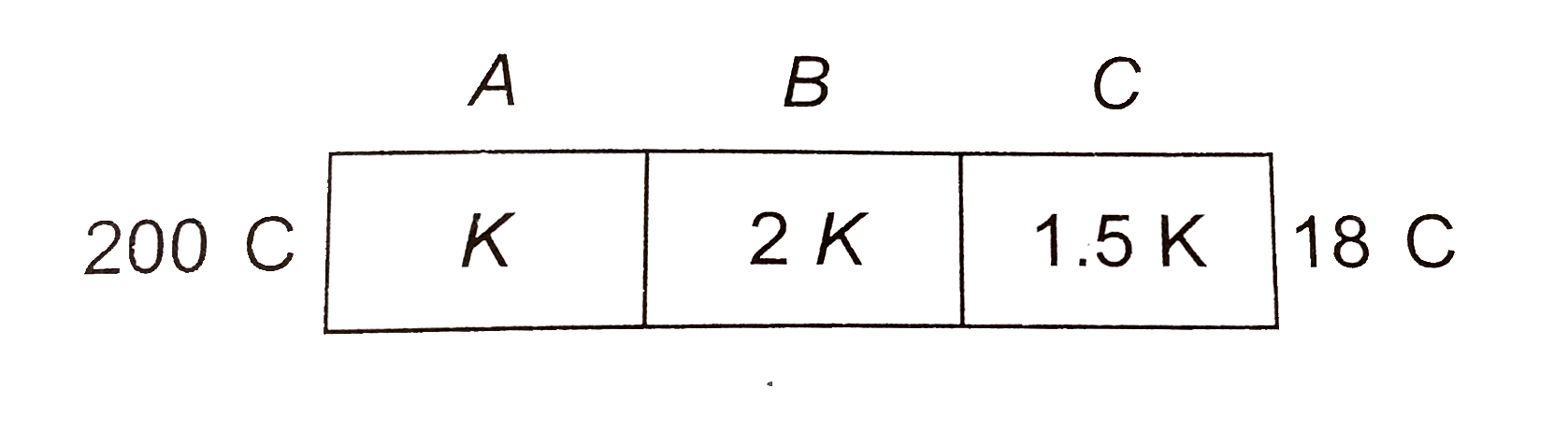 A74∘CB116∘CC156∘CD148∘C
A74∘CB116∘CC156∘CD148∘C - Question 3 - Select One
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
Three rods of the same length and the same area of the cross-section are joined. The temperature of two ends one T1 and T2 as shown in the figure.
 As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
As we move along the rod the variation of temperature are as shown in the following [Rods are insulated from the surrounding except at the faces]
 View Solution
View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thicknesses x and 4x, respectively are T2 and T1(T2>T1). The rate of heat of heat transfer through the slab, in ? steady state is [(AT2−T1x]f, with f equal to :-
 View Solution
View SolutionA hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T_(2)gtT_(1)(b)the∈softhetubeisma∫a∈edattemperatureT_(1)andtheoutsisma∫a∈edatT_(2) .
View SolutionFind the heat current through the frustum of a cone shown in figure-4.20. Temperature of its two ends are maintained at T1 and T2(T_(2)>T_(1)) respectively and the thermal conductivity of the material is k.
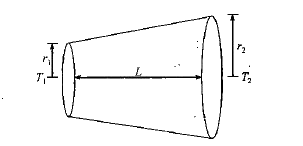 View Solution
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and seconds rods are maintained at θ1 and θ2 respectively. The temperature of the common junction is
View Solution

