A metal rod of length 2 m has cross sectional areas 2 A and A as shown in figure. The ends are maintained at temperatures 100° C and 70° C . The temperature at middle point C is

80∘C
85∘C
90∘C
95∘C
The correct Answer is:C
Let T be temperature of middle point C and in series rate of heat flow is same
⇒K(2A)(100−T)=KA(T−70)
⇒200−2T=T−70⇒3T=270⇒T=90∘C
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Check points 16.4
Explore 25 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Taking it together
Explore 47 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Check point 16.2
Explore 10 Videos
- CALORIMETRY & HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY & HEAT TRANSFERExercise:Level 2 Subjective
Explore 14 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
Similar Questions
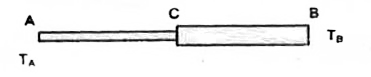
Two rods of same length and same material having area of cross section A and 4A respectively are joined as shown in the figure. If TA and TB are temperatures of free ends in steady state. The temperature of junction point C is (Assume no heat loss wil take place through lateral surface)
View SolutionThree rods AB,BC and BD made of the same materical and having the same area of cross section have been joined as shown is the The ends A,C and D are held at temperatures 20∘C Cand 80∘C respectively If each rod is of same length then find the temperature at the junction B of the three rods
 .
.
View Solution
Knowledge Check
Five identical rods are joined as shown in figure. Point A and C are maintained at temperature 120°C and 20°C respectively. The temperature of junction B will be
 A100∘CB80∘CC70∘CD0∘C
A100∘CB80∘CC70∘CD0∘C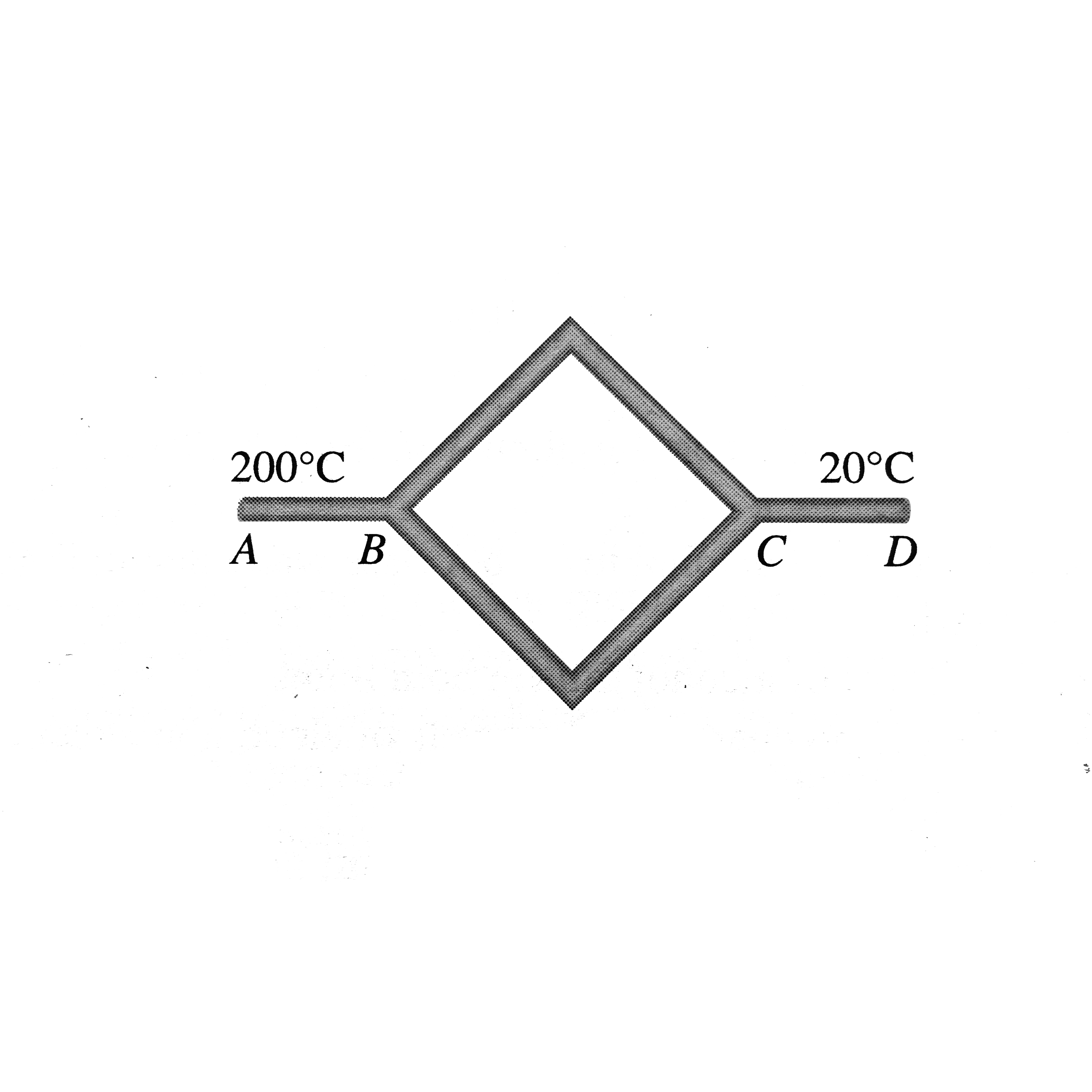
Six identical cunducting rods are joined as shown in Fig. Points A and D are maintained at temperatures 200∘C and 20∘C respectively. The temperature of junction B will beA120∘CB100∘CC140∘CD80∘CTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 A2πB1πCπDπ2
A2πB1πCπDπ2
Two identical conducting rods AB and CD are connected to a circular conducting ring at two diametrically opposite points B and C, the radius of the ring is equal to the length of rods AB and CD. The area of cross-section, thermal conductivity of the rod and ring are equal. points A and D are maintained at temperatures of 100∘C and 0∘C. temperature at poimt C will be

View SolutionTwo rods of different materials having differnet lengths and same cross sectional areas are joined end to end in a straight line. The free ends of this compound rod are maintained at different temperatures The temperature gradient in each rod will be .
View SolutionThree rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC right angled at B as shown in the figure. The points A and B are maintained at temperature T and (√2)T respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C will be

View SolutionThree rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
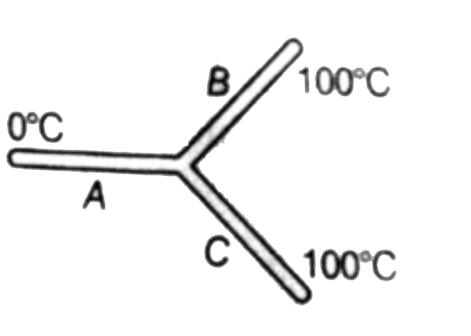
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will be
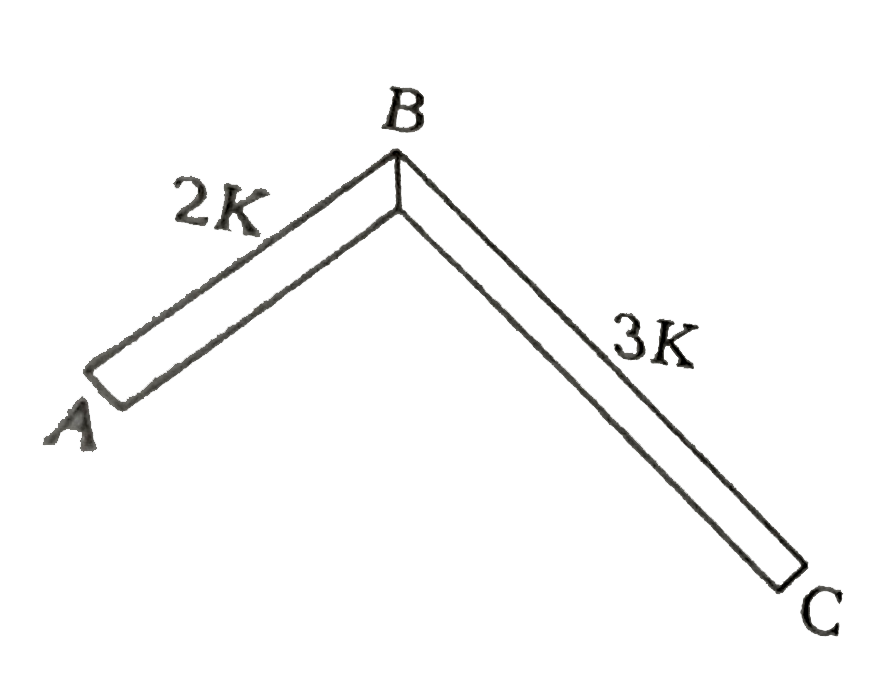
View SolutionIn the figure ABC is a conducting rod whose lateral surfaces are insulated. The length of the section AB is one-half of that of BC, and the respective thermal conductivities of the two sections are as given in the figure. If the ends A and C are maintained at 0∘C and 70∘C respectively, the temperature of junction B in the steady state is
View Solution
