Match the following columns,
Column1Column2a Thermal resitancep [MT^(-3)K^(-4)]b Stefan's constantq [M^(-1)L^(-2)T^(3)K]c Wien's constantr [ML^(2)T^(-3)]d Heat currents [LK]
The correct Answer is:A, B, C, D
Step by step video, text & image solution for Match the following columns, {:("Column1","Column2"),("a Thermal resitance","p [MT^(-3)K^(-4)]"),("b Stefan's constant","q [M^(-1)L^(-2)T^(3)K]"),("c Wien's constant","r [ML^(2)T^(-3)]"),("d Heat current","s [LK]"):} by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Assertion and reason17videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective14videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
Similar Questions
Match the following columns, Column1Coloumn2a Specific heatp [MLT^(-3)K^(-1)]b Coefficient of thermal conductivityq [MT^(-3)K^(-4)]c Boltzmann constantr [L^(2)T^(-2)K^(-1)]d Stefan's constats [ML^(2)T^(-2)K^(-1)]
View SolutionMatch the following columns.
Column IColumn IIA.Teslap[ML2A−2T−2]B.Weberq[MLA−2T−1]C.Weber m−2q.[MA−1T−2]D.Henrys.NoneView Solution
Knowledge Check
- Question 1 - Select One
Match the following two columns.
Column IColumn IIA.Electrical resistance1.[ML3T−3A−2]B.Electrical potential2.[ML2T−3A−2]C.Specific resistance3.[ML2T−3A−1]D.Specific conductance4.NoneAA-2, B-3, C-1, D-4BA-2, B-4, C-3, D-1CA-1, B-2, C-4, D-3DA-1, B-3, C-2, D-4 - Question 2 - Select One
Make the pairs
A.Thermal conductivity(i)MLT−3K−1B.Thermal resistance(ii)M−1L−2T3KC.Stefan's constant(iii)MT−3K−4D.Wien's constant(iv)LKA ABCD.(i)(ii)(iii)(iv)B ABCD.(ii)(i)(iv)(iii)C ABCD.(iv)(iii)(ii)(i)D ABCD.(iv)(ii)(iii)(i)
Match the physical quantities given on column I with dimensions expressed in terms of mass (M) length (L) time (T), and charge (Q) given in column II and write the correct answer against the matched quantity in a tabular form in your answer book.
Column-IColumn-IIAngular momentum[ML2T−2]Latent heat[ML2Q−2]Torque[ML2T−1]Capacitance[ML3T−1Q−2]Inductance[M−1L−2T2Q2]Resistivity[L2T−2]View SolutionMatch the physical quantities given in Column 1 with dimensions expressed in terms of mass (M), length (L), time (T), and charge (Q) given n column II.
Column-IColumn-II(a)Angular momentum(p)[ML2T−2](b)Torque(q)[ML2T−1](c)Inductance(r)[M−1L−2T2Q2](d)Latent heat(s)[ML2Q−2](e)Capacitance(t)[ML3T−1Q−2](f)Resistivity(u)[L2T−2]View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
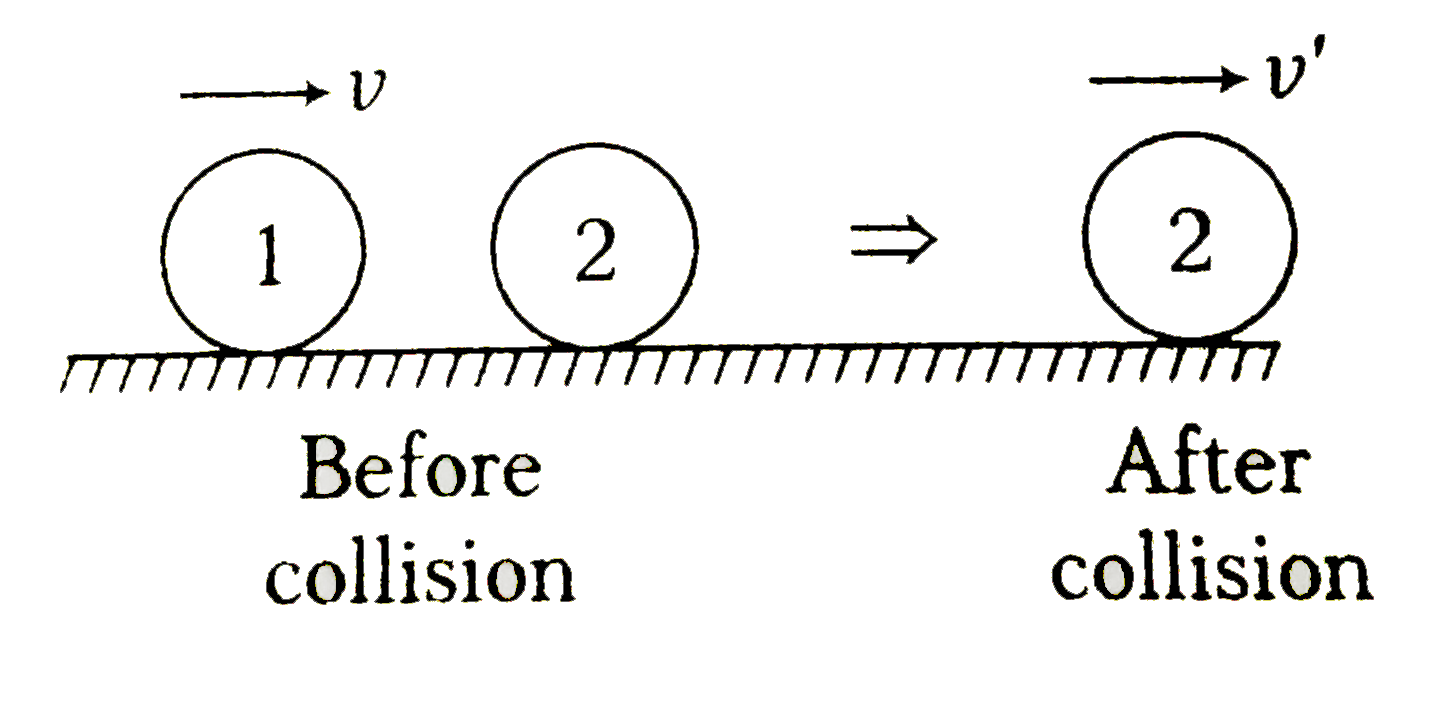
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficientView SolutionColumn IColumn II(A)Electrical resistance(p)[M−1L−2T4A2](B)Capacitance(q)[ML2T−2A−2](C)Magnetic field(r)[ML2T−3A−2](D)Inductance(s)[MT−2A−1]
View SolutionMatch the physical quantities in column A with their dimensional formula expressed in column B
ColumnAColumnB(1)Anguar Momentum(a)ML2T−2(2)Latent Heat(b)ML2T−2A−2(3)Torque(c)ML2T−1(4)Capacitance(d)ML3T−3A−2(5)Inductance(e)M−1L−2T4A2(Resistivity(f)ML2T−2A−1(7)Magnetic(g)ML−1T−2(8)Magnetic(h)L2T−2View SolutionMatch the following:
Column-I Column-II(a)F=Asin(Bt)+1Cln(Dx)For above equation to be dimensionally correct(p)[A]=[M1L1T−1],[B]=[M0L0T−1],[C]=[M0L0T−1](b)Pressure=P+12ρv2+gX(q)[A]=[M0L1T−1],[B]=[M0L0T−1],[C]=[M0L0T−1],(c)X=At+vBln(Cr)(r)[A]=[M1L1T−2],[B]=[M0L0T−1],[C]=[M−1L0T1](s)Dimensionally incorrect
(Where F = force, P = pressure, ρ = density, t = time, v = velocity, a = acceleration, X = displacement)View Solution

