A particle is attached by means of two equal strings to two points A and B in the same vertical line and describes a horizontal circle with a uniform angular speed. If the angular speed of the particle is 2√2g/h with AB=h, show that the ratio of the tensions of the strings is 5:3
Step by step video & image solution for A particle is attached by means of two equal strings to two points A and B in the same vertical line and describes a horizontal circle with a uniform angular speed. If the angular speed of the particle is 2sqrt(2g//h) with AB=h, show that the ratio of the tensions of the strings is 5:3 by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Practice Exercise
42 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question
31 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A particle of mass 21 g attached to a string of 70cm length Keeping the string always taut the ball describes a horizontal circle of radius 15cm Calculate the angular speed of the ball .
View SolutionTwo particles each of mass m are moving in horizontal circle with same angular speed. If both string are of same length then the ratio of tension in string T1T2 is
View Solution
Knowledge Check
A particle P is attached by means of two equal strings to two points A and B is same vertical line and describes horizontal circle with uniform angular speed 2√2gh where AB = h
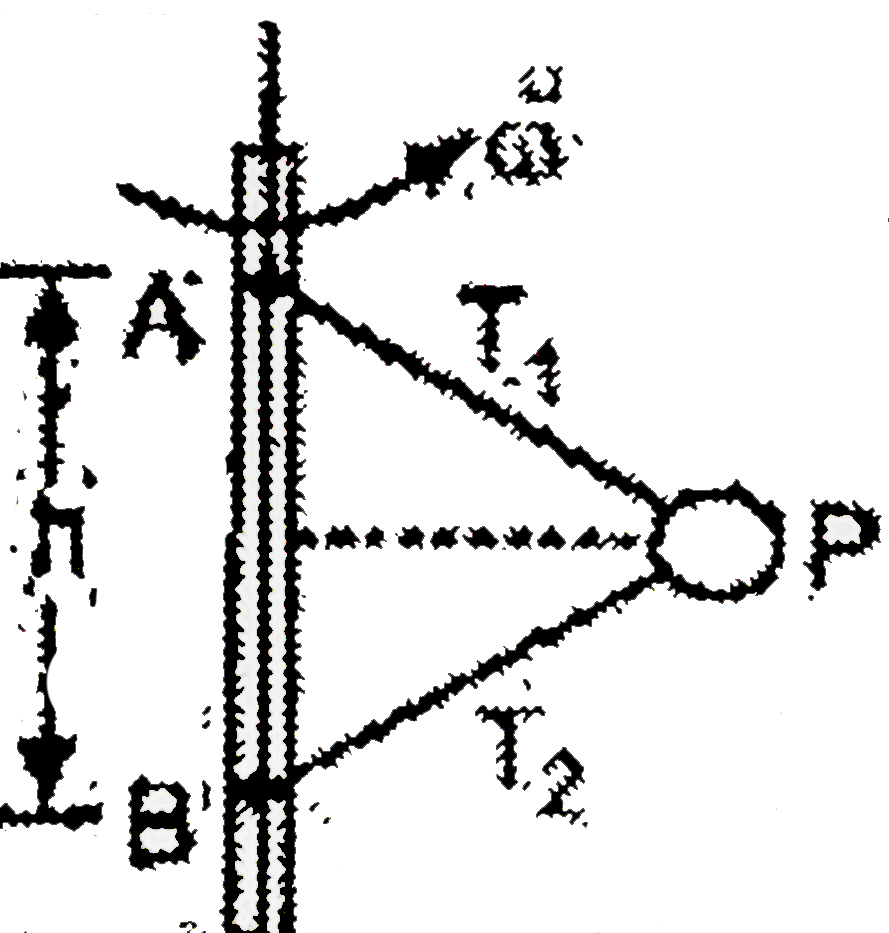 AT1>T2BT1:T2=5:3CT1:T2=√5:√3DT1=T2
AT1>T2BT1:T2=5:3CT1:T2=√5:√3DT1=T2A particle is attached by a light string of length 3 a to a fixed point and describes a horizontal circle of radius a with uniform angular velocity ω If, when the particle is moving in this manner, is suddenly stopped and then let go,find its velocity when the string is vertical in its subsequent motion :
A[2ga(3−2√2)]1/2B2ga(3−2√2)Cga(3−2√2)D2ga3−2√2A stone tied to a string of length l is whirled in a horizontal circle at a constant angular speed ω in a circle of radius r. If the string makes an angle θ with vertical then the tension in the string is :
Am(gcosθ+ω2r)Bm√ω4r2+g2Cm√ω2r2+g2Dm(gcosθ−ω2r)
A ball of mass 100 g is suspended by a string 40cm long. Keeping the string taut, the ball describes a horizontal circle of radius 10 cm. Find the angular speed.
View SolutionA heavy particle of mass 2kg is tied to two strings, each of length 25 cm and they are tied to two points 30 cm apart on the same vertical line. The particle is whirled in a horizontal plane with a speed of 1.8ms−1. Calculate the ratio of the tensions of the two strings.
View SolutionA particle, held by a string whose other end is attached to a fixed point C, moves in a circle on a horizontal frictionless surface. If the string is cut, the angular momentum of the particle about the point C
View SolutionA heavy particle hanging from a string of length l is projected horizontally with speed √gl. Find the speed of the particle at the point where the tension in the string equals weight of the particle.
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View Solution
