A particle of mass m approaches a region of force starting from r=+∞ The potential energy function in terms of distance r from the origin is given by,
U(r)=K2a3(3a2−r2)for0<r<a
=K/rforr>a
(a) Derive the force F(r) and determine whether it is repulsive or attractive.
(b) With what velocity should the particle start at r=∞ to cross over to other side of the origin.
(c) If the velocity of the particle at r=∞ is √2Kam towards the origin describe the motion.
The correct Answer is:[(a)reps–ive(b)sqrt((3K)/(am))]
Step by step video, text & image solution for A particle of mass m approaches a region of force starting from r=+infty The potential energy function in terms of distance r from the origin is given by, U(r) = K/(2a^(3))(3a^(2)-r^(2)) for 0 lt r lt a =K//r for r gt a (a) Derive the force F(r) and determine whether it is repulsive or attractive. (b) With what velocity should the particle start at r=infty to cross over to other side of the origin. (c) If the velocity of the particle at r= infty is sqrt((2K)/(am)) towards the origin describe the motion. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - Discussion Question31videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ158videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical63videos
RIGID BODIES AND ROTATIONAL MOTION
Similar Questions
The potential energy of a two particle system separated by a distance r is given by U(r)=Ar where A is a constant. Find to the radial force Fr, that each particle exerts on the other.
View SolutionA particle of mass m moves under the action of a central force. The potential energy function is given by U(r)=mkr3 Where k is a positive constant and r is distance of the particle from the centre of attraction. (a) What should be the kinetic energy of the particle so that it moves in a circle of radius a0 about the centre of attraction? (b) What is the period of this circualr motion ?
View Solution
Knowledge Check
- Question 1 - Select One or More
The potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
AThe equilibrium distance will be r0=2ABBThe equilibrium distance will be r0=3ABCIf the total energy of the particle is B26A, then its radial velocity will vaishh ate r03, where r0 is the equilibrium distanceDIf the total energy of the particle is B26A, then its radial velocity will vanish at r02,where r0 is the equilibrium distance. - Question 2 - Select One or More
A particle of mass m lies at a distance r from the centre of earth. The force of attraction between the particle and earth as a function of distance is F(r ),
AF(r)∝1r2 for r<RBF(r)∝1r2 for r≥RCF(r)∝r for r<RDF(r)∝1r for r<R - Question 3 - Select One
A shell of mass M and radius R has point mass m placed at a distance r from its centre. The gravitational potential energy U(r) vs r will be
A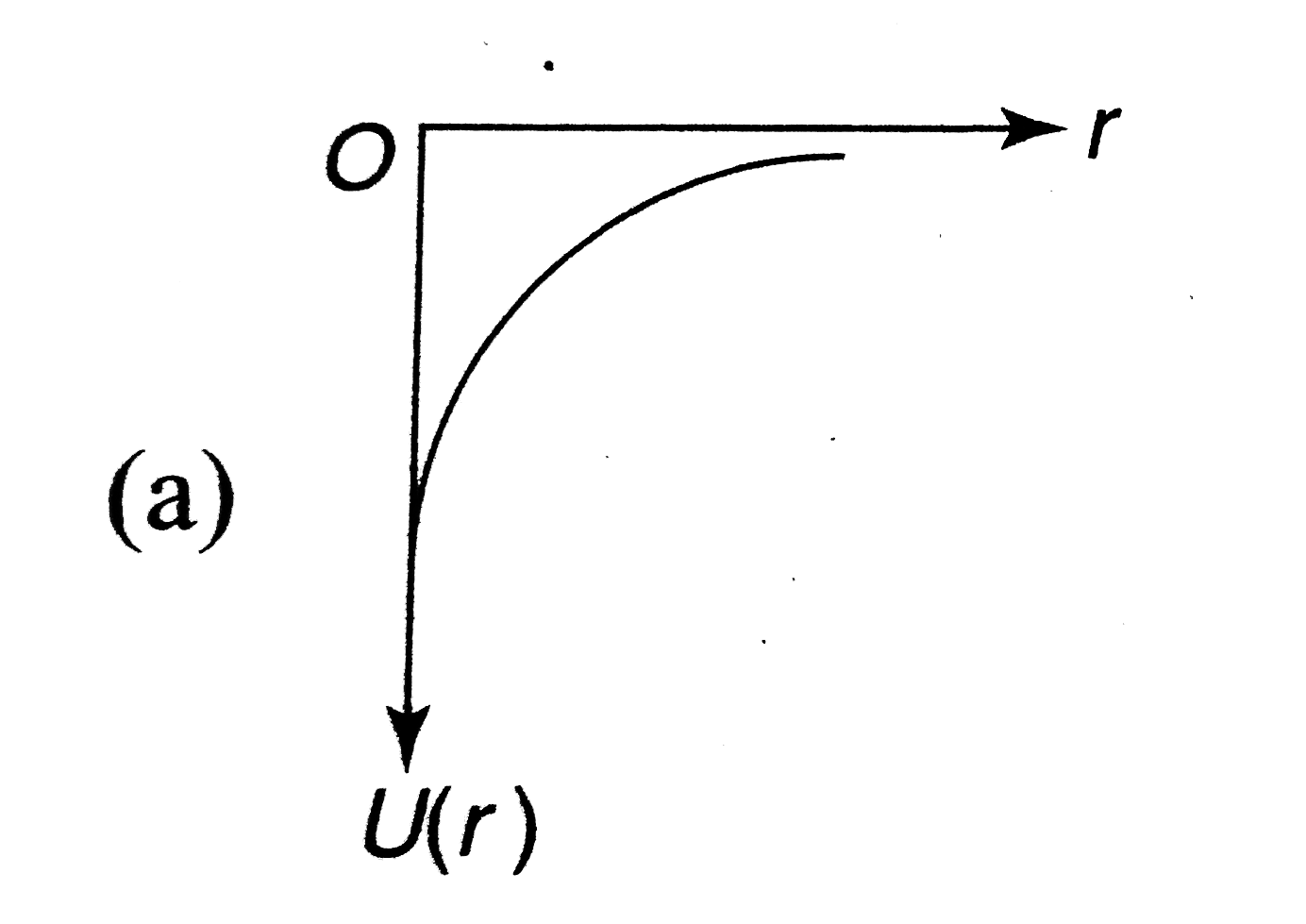 B
B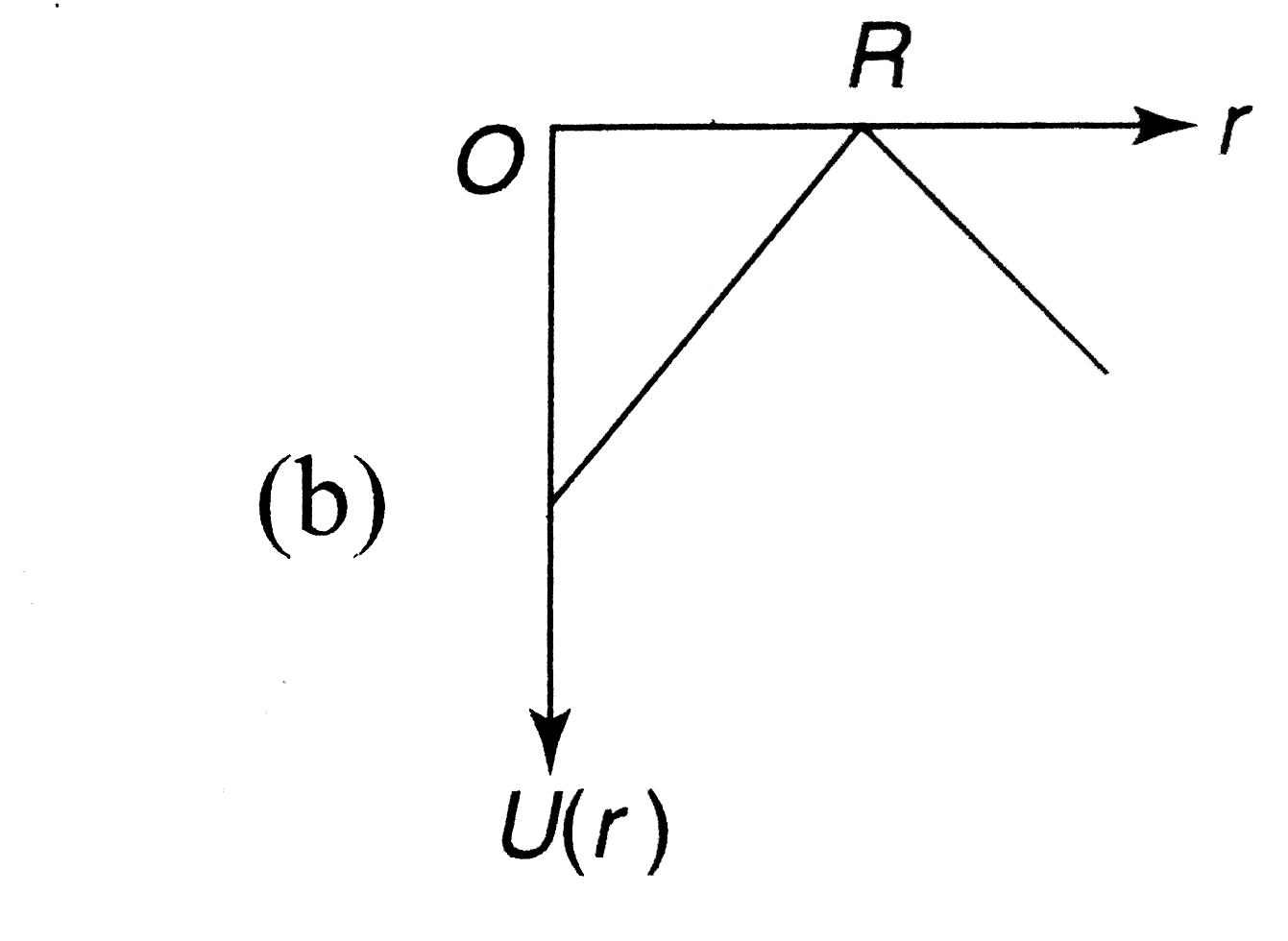 C
C D
D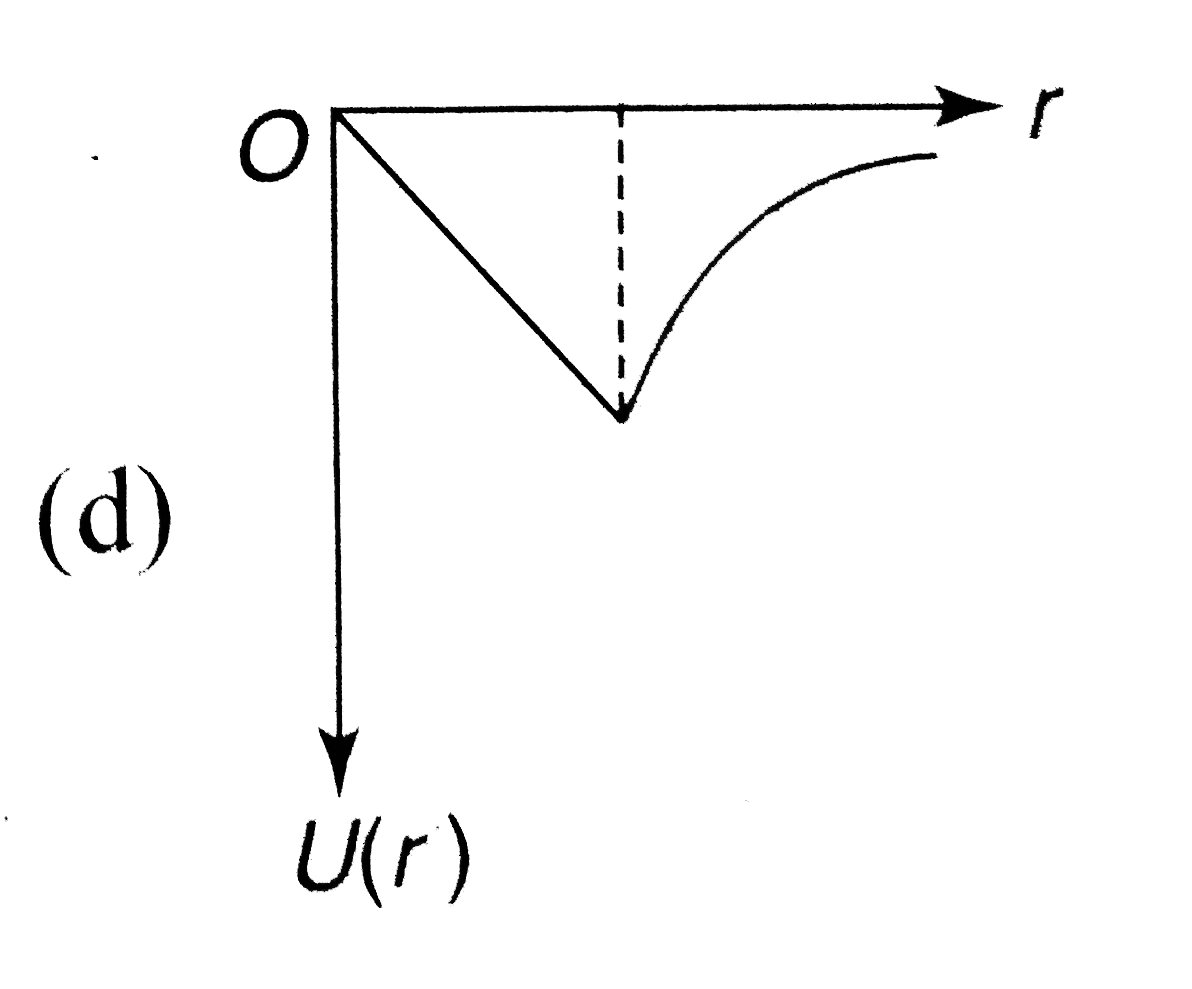
The potential energy function for the force between two atoms in a diatomic molecule is approximate given by U(r)=ar12−br6, where a and b are constants and r is the distance between the atoms. If the dissociation energy of the molecule is D=[U(r=∞)−Uat equilibrium],D is
View SolutionAll the particles are situated at a distance R from the origin. The distance of centre of mass of the body from the origin will be
(1) More than R
(2) Less than R
(3) Equal to R
(4) At the originView SolutionIF a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (−Kr2) , then its total energy is
View SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
If the total energy of the particle is E=−3B216A, and it is known that the motion is radial only then the velocity is zero atView SolutionIn a conservative force field we can find the radial component of force from the potential energy function by using F=−dUdr. Here, a positive force means repulsion and a negative force means attraction. From the given potential energy function U(r ) we can find the equilibrium position where force is zero. We can also find the ionisation energy which is the work done to move the particle from a certain position to infinity.
Let us consider a case in which a particle is bound to a certain point at a distance r from the centre of the force. The potential energy of the particle is : U(r)=Ar2−Br where r is the distance from the centre of the force and A andB are positive constants. Answer the following questions.
The work required to move the particle from equilibrium distance to infinity isView Solution

