Consider a spring that does not obey Hook's law. One end of the spring is held fixed. When it is stretched or compressed by an amount x, the force it exert is F=ax−bx+cx2 Where a=50N/mb=150N/m2 and c=5000N/m3 How much work must be done to stretch this spring by 1m from its unstretched length ?
The correct Answer is:A
Step by step video, text & image solution for Consider a spring that does not obey Hook's law. One end of the spring is held fixed. When it is stretched or compressed by an amount x, the force it exert is F=ax-bx+cx^(2) Where a=50N//m b=150N//m^(2) and c=5000N//m^(3) How much work must be done to stretch this spring by 1m from its unstretched length ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ158videos
WORK, ENERGY AND POWER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical63videos
RIGID BODIES AND ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A force acting on a particle varies with the displacement x as F=ax−bx2. Where a=1 N/m and b= 1 N/m2. The work done by this force for the first one meter (F is in newtons, X is in meters) is :
A16JB26 JC36 JDNone of these - Question 2 - Select One
When a rubber-band is stretched by a distance x, it exerts a restoring force of magnitude F=ax+bx2 where a and b are constants. The work done in stretching the unstretched rubber band by L is :
AaL22+bL33B12(aL22+bL33)CaL2+bL2D12(aL2+bL2) - Question 3 - Select One
When a 4kg mass in hung vertically from a light spring that obeys Hooke's low, the spring stretches by 2 cm. The work that should be done by an external agent in stretching this spring by 5 cm will be (use g=10m/s2)
A1.5 JB1.75 JC2 JD0.9 J
A force of 20.0 N is required to hold a spring stretched by 5.0 cm from its equilibrium position. How much work was done in stretching the spring ?
View SolutionIn figure a spring with k=168N/m is in its relaxed length and is at the top of a frictionless incline of angle θ=37∘. The lower end of the incline is at distance D = 1 m from the end of the spring. A small blcok of mass 2 kg is pushed against the spring until the spring is compressed by 0.2 m and released from rest.
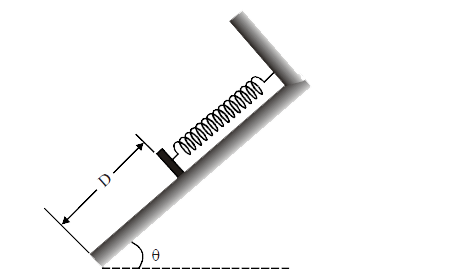
What is the speed of the block at the instant the spring returns to its relaxed length (which is when the block loses contact with the spring)?View SolutionA 1.0 kg block moving at 8.0 m/s strikes a spring fixed at one end to a wall and compresses the spring by 0.40 m, where its speed gets reduced to 2.0 m/s. After this event, the spring is mounted upright by fixing its bottom end to afloor, and a stone of mass 2.0 kg is placed on it, the spring is now compressed by 0.50 m from its rest length. The system is then released. How far above the rest-length point does the stone rise ?
View SolutionIn the adjoining diagram the ball A is released from rest when the spring is at its natural length (neither stretched nor compressed) For the block B of mass M to leave contact with the ground at some time, the minimum mass of A must be:
 View Solution
View SolutionA spring of spring constant 5×102Nm is streched initially by 5cm from the unstriched position . Then the work required to streach is further by another 5cm is
View Solution

