A heavy particle is suspended by a light thread, the other end of the thread being fixed to a point O. The particle is projected from its lower position in the horizontal direction in the vertical plane through O, with such a velocity that it leaves the circular path after an angular displacement θ Show that when the string again becomes taut it makes an angle 3θ−360∘ with the downward drawn vertical.
The correct Answer is:A
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
158 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical
63 Videos
Similar Questions
A particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
View SolutionA heavy particle is attached to one end of a light string of length l whose other end is fixed at O. The oarticle is projectyed horizontally with a velocity v0 from its lowest position A. When the angular displacement of the string is more than90∘, the particle leaves the circular path at B. The string again becomes taut at C such that B,O,C are collinear. Find v0 in terms of l and g
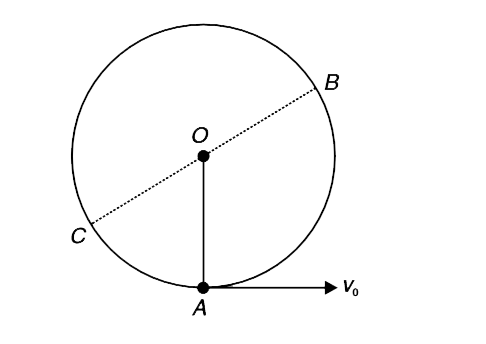
View Solution
Knowledge Check
A heavy particle is attached to one end of a string 1m long whose other end is fixed at O. It is projected from it lowest position horizontally with a velocity V:
AIf V2>5 g the particle will describe complete circular motion in the vertical planeBIf V2=3.5 g the tension in the string will become zero after the string has turned through 120∘CIf V2=2 g, the tension in the string becomes zero the velocity of the particle also becomes zeroDIf V2=g the velocity of the particle becomes zero after the string turns through 60∘A particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
A30∘B90∘C120∘D150∘A particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
A30∘B135∘C120∘D150∘
A particle suspended from a fixed point, by a light inextensible thread of length L is projected horizontally from its lowest position with velocity 7gL . The thread will slack after swinging through an angle , such that equal
View SolutionA particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View Solution
