Find the value of area of rectangle PQRS

If perimeter of rectangle & Parallelogram is equal with same base. Find the ratio of area of rectangle and area of parallelogram.
A $= 1$
B $> 1$
C $< 1$
DNone of these
PQRS is a rectangle. T is a point on PQ such that RTQ is an isosceles triangle and PT = 5 QT.If the area of triangle RTQ is $12 \sqrt{3}$ sq.cm, then the area of the rectangle PQRS is:
A $142 \sqrt{3} s q . c m$
B $134 \sqrt{3} s q . c m$
C $144 \sqrt{3} s q . c m$
D $142 s q . c m$
PQRS is a rectangle. When the length and breadth of the rectangle increases, the rectangle is enlarged to VWRT and the area of the rectangle is enlarged by $226 c m^{2}$ . If the length of rectangle PQRS is twice its breadth. Find
(i) Perimeter of rectangle PQRS.
(ii) Area of rectangle VWRT.

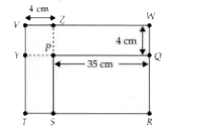A(i) - 105 cm, (ii) $388.5 c m^{2}$
B(i) - 105 cm, (ii) - $838.5 c m^{2}$
C(i) - 108 cm, (ii) - $838.5 c m^{2}$
D(i) - 108 cm, (ii) - $388.5 c m^{2}$

If perimeter of rectangle & Parallelogram is equal with same base. Find the ratio of area of rectangle and area of parallelogram.