If two parallel chords of a circle, having diameter 4 units, lie on the opposite sides of the centreand subtend angles cos−1(17)andsec−1(7) at the centre respectively, then the distance betweenthese chords, is: (a) 4√7 (b) 8√7 (c) 87 (d) 167
Step by step video & image solution for If two parallel chords of a circle, having diameter 4 units, lie on the opposite sides of the centreand subtend angles cos^-1(1/7) and sec^-1(7) at the centre respectively, then the distance betweenthese chords, is: (a) 4/sqrt7 (b) 8/sqrt7 (c) 8/7 (d) 16/7 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
If two parallel chords of a circle, having diameter 4 units, lie on the opposite sides of the centreand subtend angles cos−1(17)andsec−1(7) at the centre respectively, then the distance betweenthese chords, is: (a) 4√7 (b) 8√7 (c) 87 (d) 167
View Solution7.The distance of the point P(1,7) from the y -axis is : (a) 1 (b) 7 (c) 6 (d) 8
View Solution
Knowledge Check
In a circle, there are two chords opposite to the centre of the circle. The length of one chord and the radius of the circle is 6 cm and 5 cm respectively, and the distance between both the chords is 7 cm. Find the length of the second chord.
Aa) 8 cmBb) 10 cmCc) 6 cmDd) 14 cmA chord of length 7 cm subtends an angle of 60∘ at the centre of a circle. What is the radius (in cm) of the circle?
A7√2B7√3C7D14A chord of length 7 cm subtends an angle of 60∘ at the centre of a circle. What is the radius (in cm) of the circle?
A7√2B7√3C7D14
Two chords AB and CD of lengths 24 cm and 10 cm respectively of a circle are parallel. If the chords lie on the same side of the centre and distance between them is 7 cm, find the length of a diameter of the circle.
View SolutionIf θ is an acute angle such that tan2θ=87 , then the value of (1+sinθ)(1−sinθ)(1+cosθ)(1−cosθ) is (a) 78 (b) 87 (c) 74 (d) 6449
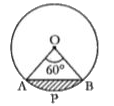
View SolutionIn a circle of radius 7 cm, a chord makes an angle of 60∘ at the centre of the circle. Find area of the circle
(Take √3=1.73)
View SolutionSolve: 1√3−8−1√8−√7
View SolutionThe radius of a circle is 6 cm. The perpendicular distance from the centre of the circle to the chord which is 8 cm in length, is
View Solution
