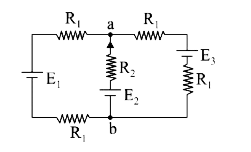
In the given network of ideal cells and resistors, R1=1.0Ω,R2=2.0Ω,E1=2V and E2=E3=4V. The potential difference between the point a and b is
83V
103V
94V
134V
The correct Answer is:B
Step by step video & image solution for In the given network of ideal cells and resistors, R_(1) = 1.0 Omega, R_(2) = 2.0 Omega, E_(1) = 2V and E_(2) = E_(3) = 4V. The potential difference between the point a and b is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
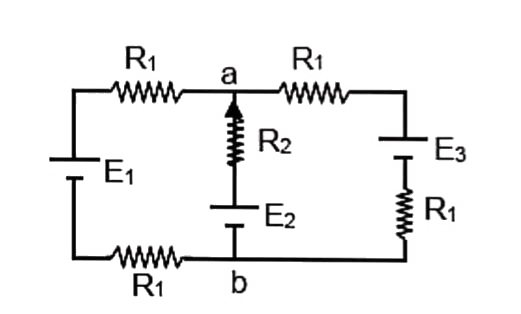
In the network shown the potential difference between A and B is (R=r1=r2=r3=1Ω,E1=3V,E2=2V,E3=1V)
 A1VB2VC3VD4V
A1VB2VC3VD4VIn the circuit shown here, E1=E2=E3=2V and R1=R2=4ohms. The current flowing between point A and B through battery E2 is
 AZeroB2amp from A to BC2amp from B to ADNone of the above
AZeroB2amp from A to BC2amp from B to ADNone of the aboveIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
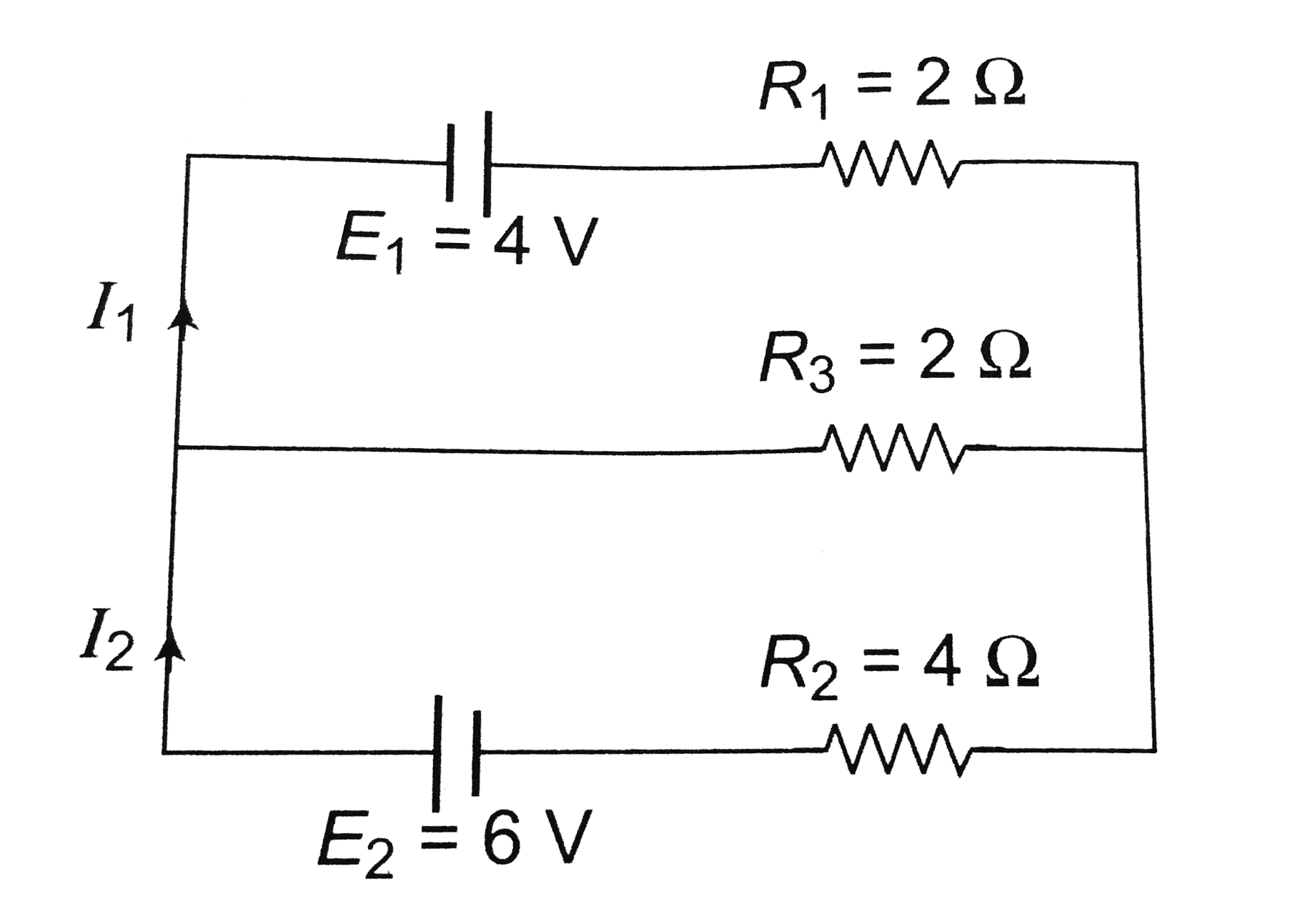 A1.6AB1.8AC1.25AD1.0A
A1.6AB1.8AC1.25AD1.0A
In the circuit shown in figure ,(ε)1=3V,(ε)2=2V,(ε)3=1Vandr1=r2=r3=1(Ω).Find the potential difference between the points A and B and the current through each branch.

View SolutionIn the circuit shown in fig. E1=3 volt,E2=2 volt,E3=1 vole and R=r1=r2=r3=1ohm.
(i) Find potential difference in Volt between the points A and B with A & B unconnected.
(ii) If r2 is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.
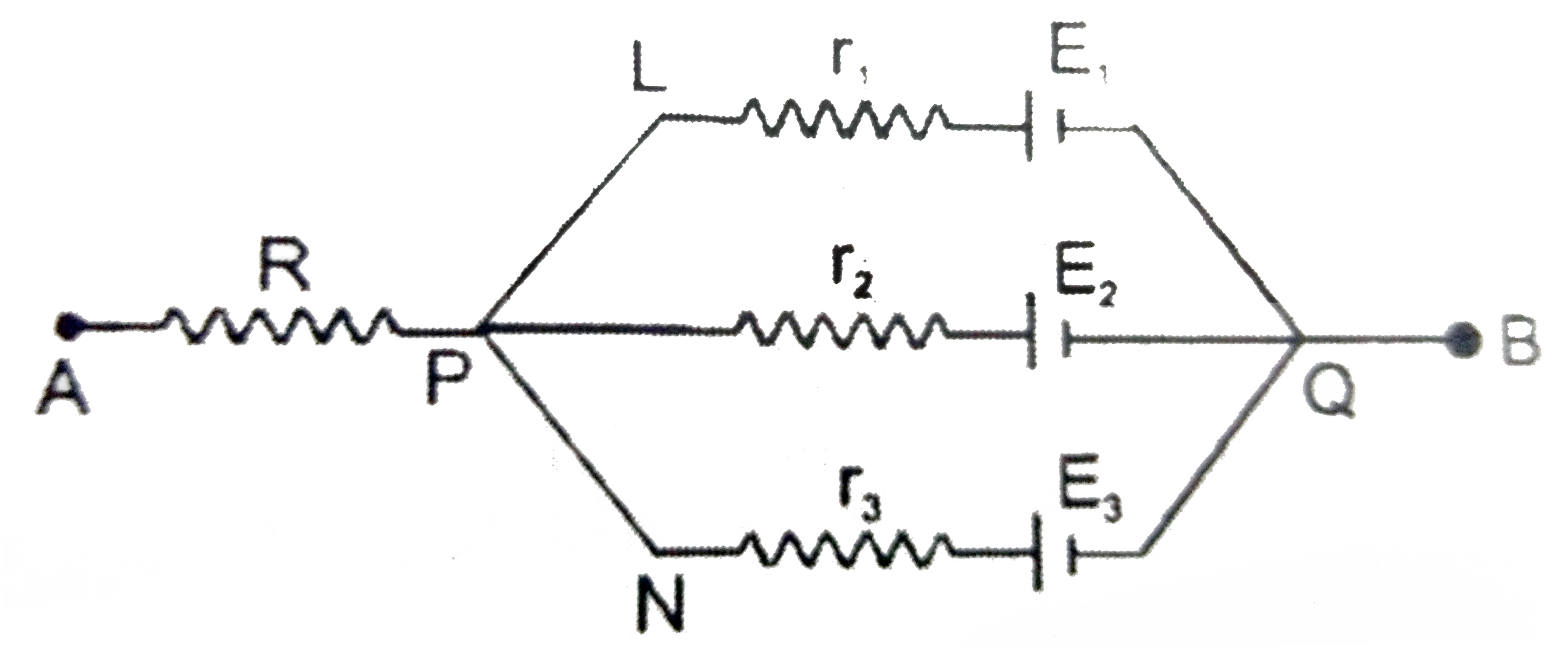
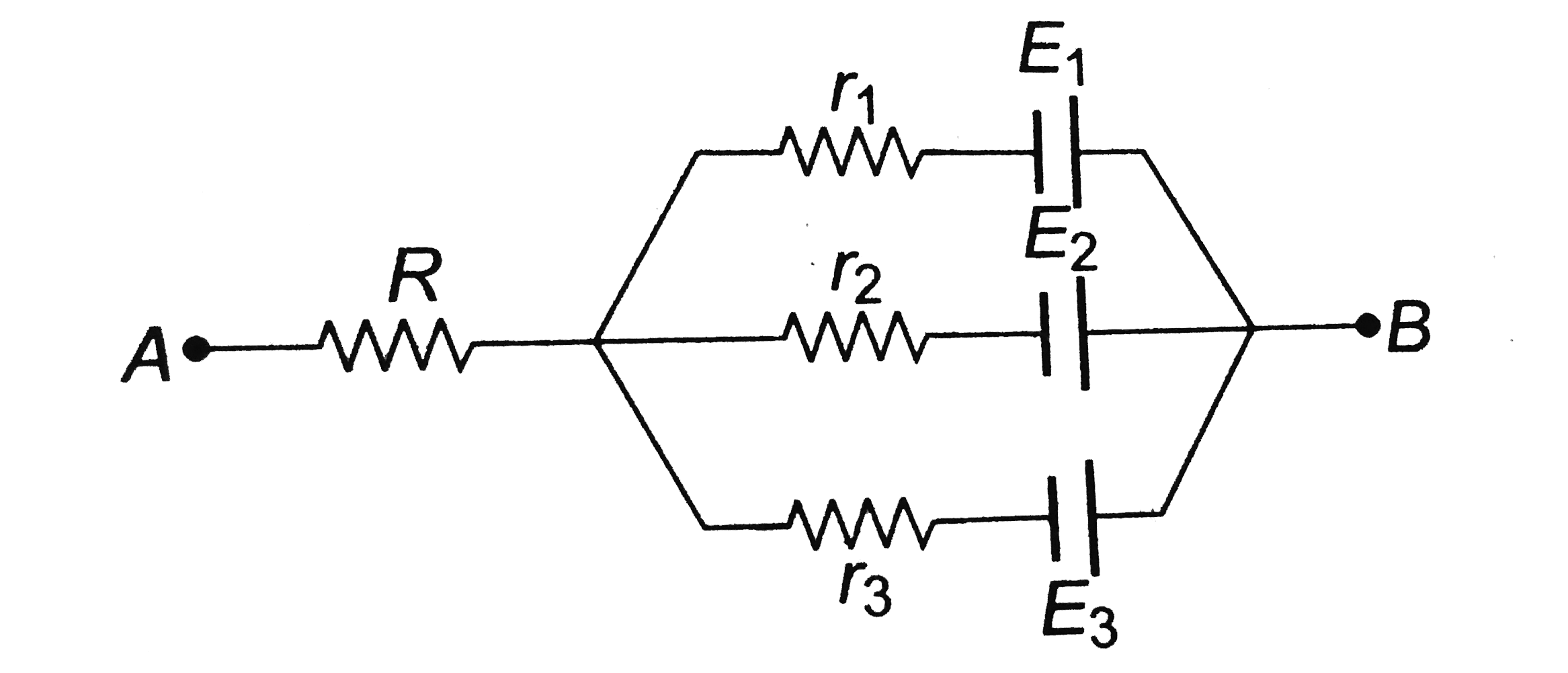
View SolutionFind a potentail difference φ1−φ2 between points 1 and 2 of the circuit shown in Fig if R11=10Ω,R2=20Ω,E1=5.0V, and E2=2.0V. The internal resisances of the current sources are negligible.

View SolutionIn the circuit shown in figure ,(ε)1=3V,(ε)2=2V,(ε)3=1Vandr1=r2=r3=1(Ω).Find the potential difference between the points A and B and the current through each branch.

View SolutionIn the circuit shown in fig E1=3vo<s,E2=2vo<s,E3=1vo<andR=r1=r2=r3=1ohm.
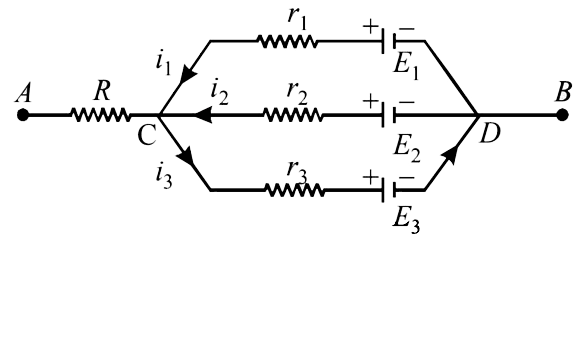
(i) Find the potential difference between the points A and B and the currents through each branch.
(ii) If r2 is short circuited and the point A is connected to point B, find the current through E1,E2,E3 and the resistor R.
View Solution