The acceleration due to gravity at a depth $R / 2$ below the surface of the earth is

g/2

g/4

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the acceleration due to gravity at a depth of $\frac{R}{2}$ below the surface of the Earth, we can use the formula for gravitational acceleration at a depth $h$ :
$g_{d} = g (1 - \frac{h}{R})$
where:
- $g_{d}$ is the acceleration due to gravity at depth $h$ ,
- $g$ is the acceleration due to gravity at the surface of the Earth,
- $h$ is the depth below the surface,
- $R$ is the radius of the Earth.
1. Identify the depth:
We are given that the depth $h = \frac{R}{2}$ .
2. Substitute the depth into the formula:
We substitute $h$ into the formula:
$g_{d} = g ⎛ ⎝ 1 - \frac{\frac{R}{2}}{R} ⎞ ⎠$
3. Simplify the fraction:
Simplifying $\frac{\frac{R}{2}}{R}$ gives:
$\frac{R}{2 R} = \frac{1}{2}$
4. Substitute back into the formula:
Now we can substitute this back into our equation:
$g_{d} = g (1 - \frac{1}{2})$
5. Calculate the result:
This simplifies to:
$g_{d} = g (\frac{1}{2}) = \frac{g}{2}$
Final Answer:
Thus, the acceleration due to gravity at a depth of $\frac{R}{2}$ below the surface of the Earth is:
$g_{d} = \frac{g}{2}$

Updated on:7/8/2024

The acceleration due to gravity at a depth d below the surface of the earth is 20% of its value at the surface. What is the value of d if the radius of the earth=6400km ?
A5120km
B4600km
C7350km
D2840km
The ratio of accleration due to gravity at a depth h below the surface of earth and at a height h above the surface of earth for h $< <$ radius of earth:
AIs constant
BChanges linearly with h
CChanges parabolically with h
DDecreases
Which of the following graphs shows the variation of acceleration due to gravity g with depth h from the surface of the earth ?

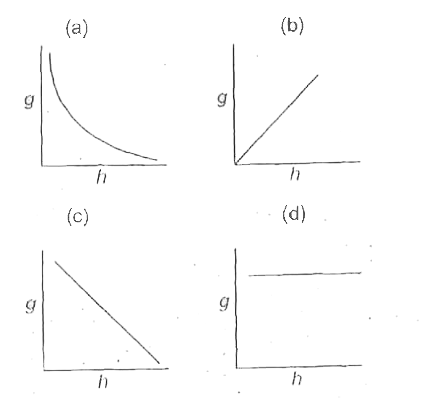A(a)
B(b)
C(c )
D(d)