Let us consider two functions f(x)=In(2x−x2)+sin(πx2)andg|x|=log|x−1|(|x|x) where {.} denotes G.I.P Match the items of Column I with those of Column II Graph of f is symmetrical about the line
Step by step video & image solution for Let us consider two functions f(x) = In(2x-x^2) + sin ((pix)/2) and g|x|=log_(|x-1|) ((|x|)/x) where {.} denotes G.I.P Match the items of Column I with those of Column II Graph of f is symmetrical about the line by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
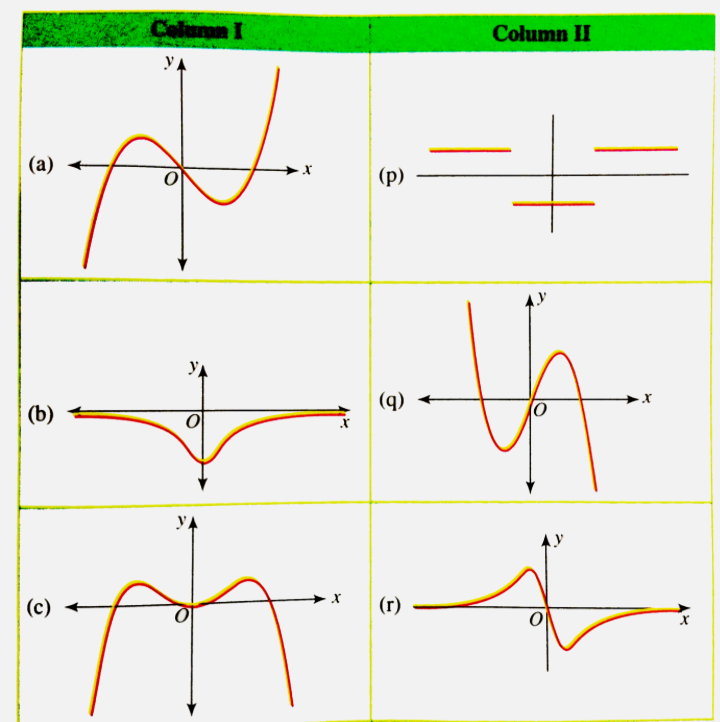
Match the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.
 02:21View Solution
02:21View SolutionLet f be a differential function such that f(x)=f(2−x) and g(x)=f(1+x) then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) f'(1)=0
03:59View SolutionThe graph of the function y = f(x) is symmetrical about the line x = 2, then
01:30View SolutionIf the graph of the function y = f(x) is symmetrical about the line x = 2, then
02:50View SolutionMatch the items in Column I with the relevant item in column II.
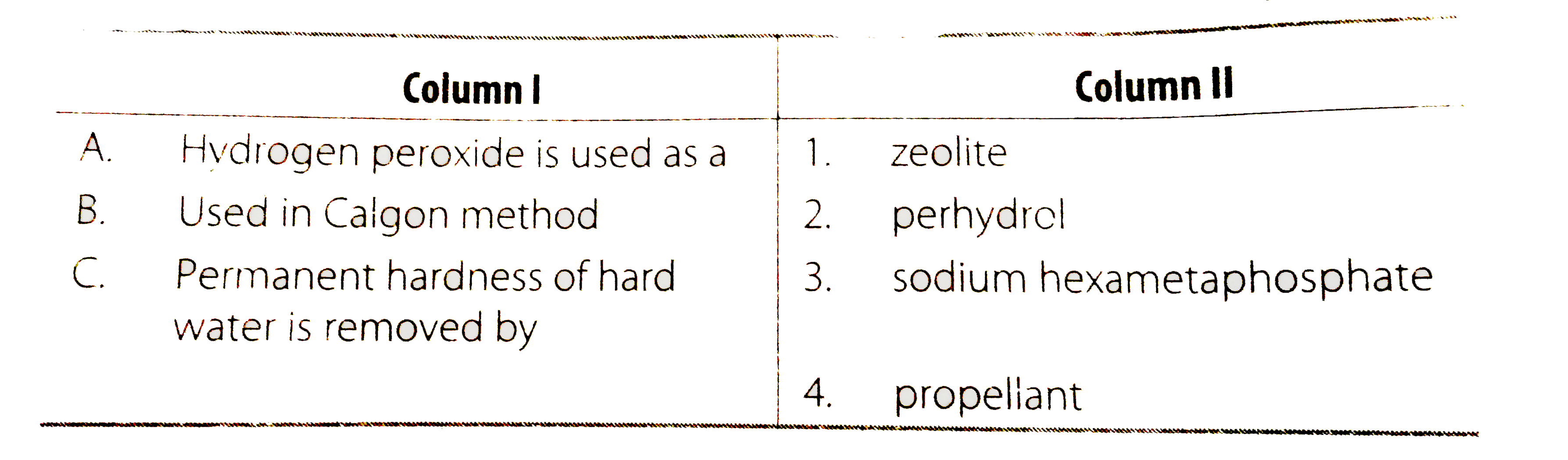 03:14View Solution
03:14View SolutionThe graph of the function y=f(x) is symmetrical about the line x=2, then :
02:59View SolutionIf the graph of the function y = f(x) is symmetrical about the line x = 2, then
01:51View SolutionFind the range of f(x)=x−[x]1−[x]+x',where[] represents the greatest integer function.
03:25View Solution

