If a vessel containing a fluid of density ρ upto height h is accelerated vertically downwards with accelerations a0. Then the pressure by fluid at the bottom of a vessel is
p=p0+ρgh+ρha0
p=p0+ρgh
p=p0+ρh(g−a0)
p=p0ρgh
To solve the problem, we need to determine the pressure at the bottom of a vessel containing a fluid of density ρ when the vessel is accelerated vertically downwards with an acceleration a0.
1. Understanding the Setup:
- We have a vessel filled with a fluid of density ρ up to a height h.
- The vessel is accelerating downwards with an acceleration a0.
2. Identify Forces Acting on the Fluid:
- The fluid experiences two main forces:
- The gravitational force acting downwards, which is g (acceleration due to gravity).
- The pseudo force acting upwards due to the downward acceleration of the vessel, which is equal to a0.
3. Effective Gravitational Acceleration:
- When the vessel accelerates downwards, the effective gravitational acceleration geffective acting on the fluid becomes:
geffective=g−a0
- This is because the downward acceleration a0 reduces the effective force acting on the fluid.
4. Calculating Pressure at the Bottom of the Vessel:
- The pressure at a depth h in a fluid is given by the hydrostatic pressure formula:
P=P0+ρgeffectiveh
- Here, P0 is the atmospheric pressure acting on the fluid surface.
- Substituting for geffective:
P=P0+ρ(g−a0)h
5. Final Expression for Pressure:
- Therefore, the pressure at the bottom of the vessel is:
P=P0+hρ(g−a0)
Conclusion:
The pressure exerted by the fluid at the bottom of the vessel is given by:
P=P0+hρ(g−a0)
- We have a vessel filled with a fluid of density ρ up to a height h.
- The vessel is accelerating downwards with an acceleration a0.
- The fluid experiences two main forces:
- The gravitational force acting downwards, which is g (acceleration due to gravity).
- The pseudo force acting upwards due to the downward acceleration of the vessel, which is equal to a0.
- When the vessel accelerates downwards, the effective gravitational acceleration geffective acting on the fluid becomes:
geffective=g−a0
- This is because the downward acceleration a0 reduces the effective force acting on the fluid.
- The pressure at a depth h in a fluid is given by the hydrostatic pressure formula:
P=P0+ρgeffectiveh
- Here, P0 is the atmospheric pressure acting on the fluid surface.
- Substituting for geffective:
P=P0+ρ(g−a0)h
- Therefore, the pressure at the bottom of the vessel is:
P=P0+hρ(g−a0)
The pressure exerted by the fluid at the bottom of the vessel is given by:
P=P0+hρ(g−a0)
Topper's Solved these Questions
- BOOK - BITSAT GUIDECHAPTER - FLUID MECHANICSEXERCISE - BITSAT Achives15videos
FLUID MECHANICS
- BOOK - BITSAT GUIDECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - All Questions33videos
ELECTROMAGNETIC INDUCTION
- BOOK - BITSAT GUIDECHAPTER - GAUSS LAW AND ELECTRIC POTENTIAL THEORYEXERCISE - BITSTAT ARCHIVES4videos
GAUSS LAW AND ELECTRIC POTENTIAL THEORY
Similar Questions
A container having a liquid of density ρ is moving downwards with acceleration g2. Find the pressure difference between two vertical points in the liquid separated by h
View Solution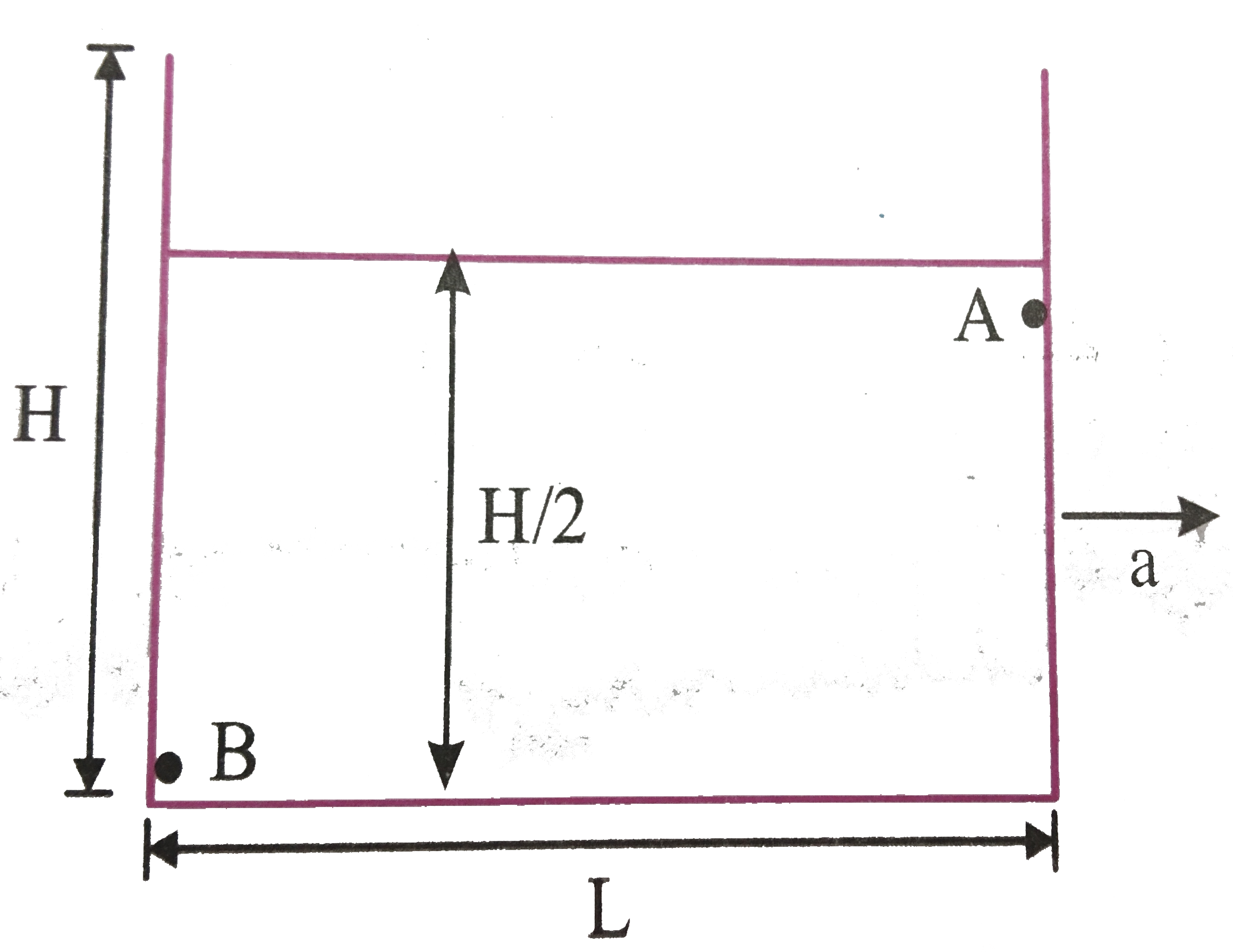
A vessel of height H and length L contains a liquid of density ρ upto height H/2 The vessel start accelerating horizontally with acceleration a towards right. If A is the point at the surface of the liquid at right . If A is the point at the surface of the liquid at right end while the vessel is accelerating and B is the point at bottom of the vessel on the other end, the difference of pressures at B and A will beView Solution
Knowledge Check
- Question 1 - Select One
In a cylindrical vessel containing liquid of density ρ there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be
 Ah2−h1Bh2+h1Ch2−h12Dh2+h12
Ah2−h1Bh2+h1Ch2−h12Dh2+h12 - Question 2 - Select One
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA)
A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA) - Question 3 - Select One
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgA
A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgA
In a cylindrical vessel containing liquid of density ρ, there are two holes in the side walls at heights of h1 and h2 respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole, for which the range of efflux would be maximum, will be –
 View Solution
View SolutionA cylinder of mass m and density ρ hanging from a string is lowered into a vessel of cross-section area s containing a liquid of density σ(<ρ) unit it is fully immersed. The increase in pressure at the bottom of the vessel is
View SolutionA block of mass m and density p is hanging from a string . If it is lowered into a vessel of cross-sectional area A containing a liquid of density σ(<ρ) and gets fully immered, the increase in pressure at the bottom of vessel would be
View Solution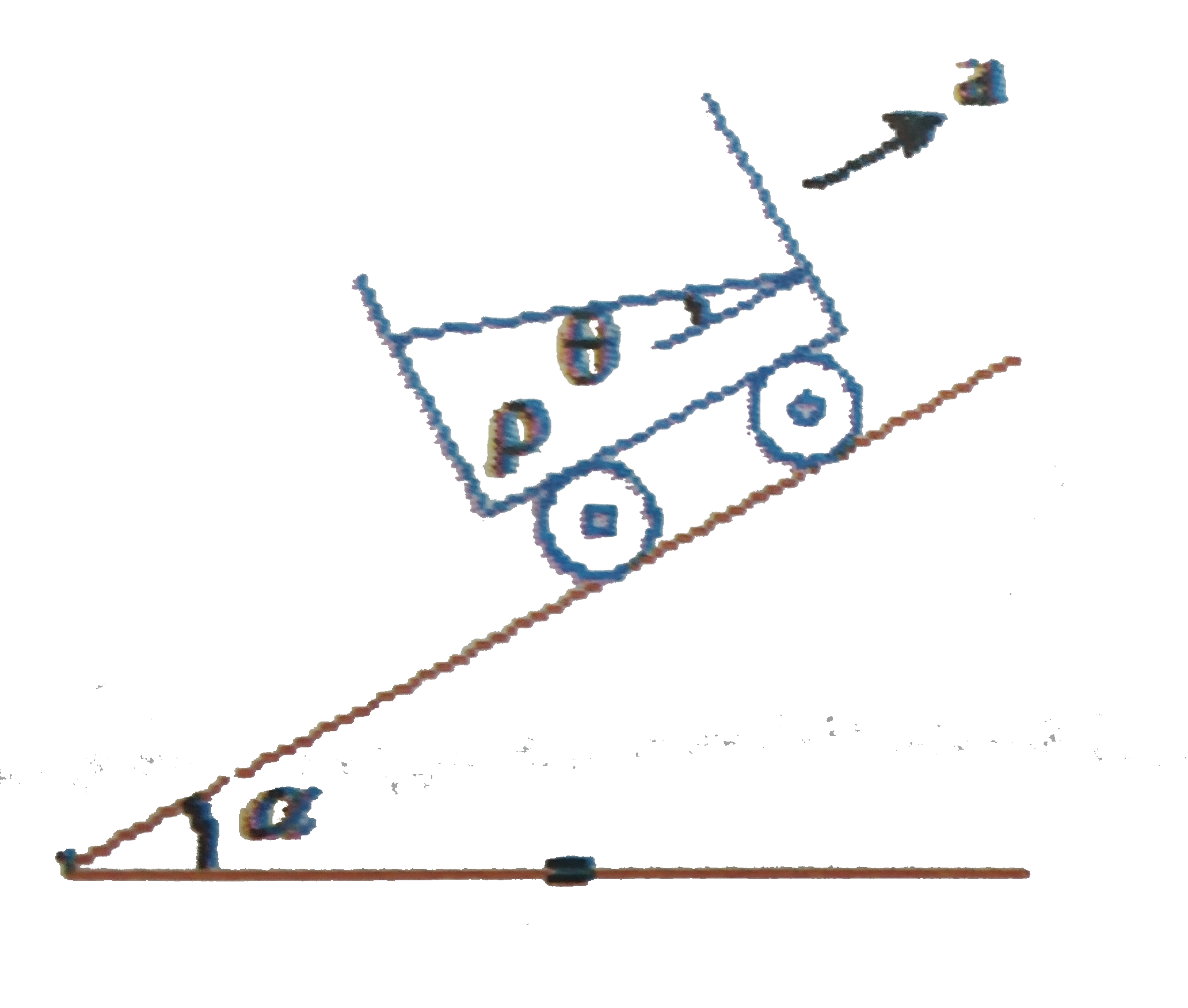
A fluid container is containing a liquid of density ρ is accelerating upward with acceleration a along the inclined plane of inclination α as shown in the figure. Then the angle of inclination θ of free surface isView Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isView Solution

