The radius of the biggest metal coin of thickness t and density $ρ$ which would be able to float on water surface of surface of water is $ρ$

A

$\frac{S}{2 ρ gt}$

B

$\frac{S}{ρ gt}$

C

$\frac{2 S}{ρ gt}$

D

$\frac{4 S}{3 ρ gt}$

Video Solution

Text Solution

Verified by Experts

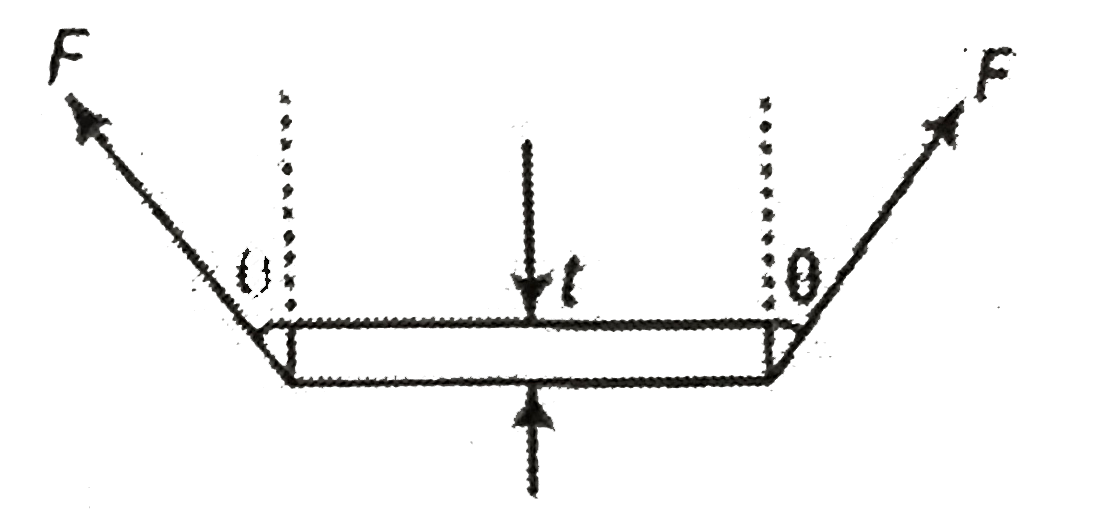
(c) For the biggest coin, the force due to surface tension shall be vertical $(i . e . θ = 0)$
$∴$ Upward force exerted on the coin at the verge of its sinking
$F = (S) \times (2 π r) (r=radius of coin)$
Now, " " F=weight of coin
$∴ S \times 2 π r = π t^{2} τ \times ρ g \Rightarrow r = \frac{2 S}{ρ gt}$

|

Updated on:21/07/2023

Class 12 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
What is the radius of the biggest aluminium coin of thickness t and density $ρ$ , which will still be able to that on the water surface of surface tension S ?
A $\frac{4 S}{3 ρ g t}$
B $\frac{3 S}{4 ρ g t}$
C $\frac{2 S}{ρ g t}$
D $\frac{S}{ρ g t}$
Question 2 - Select One
Microscopicorganism which passively float on the surfac of water is called
APhytoplantons
BZooplantones
Ca &b both
DNone of these
Question 3 - Select One
Radius of the earth is R and the mean density is $ρ$ . Find out the gravitational potential at the earth's surface
A $- \frac{4}{3} π G ρ R^{2}$
B $- 2 π G ρ R^{2}$
C $- \frac{1}{3} π G ρ R^{2}$
D $- \frac{2}{3} π G ρ R^{2}$

BITSAT GUIDE-FLUID MECHANICS-BITSAT Achives

Home
Ask Doubt
Profile