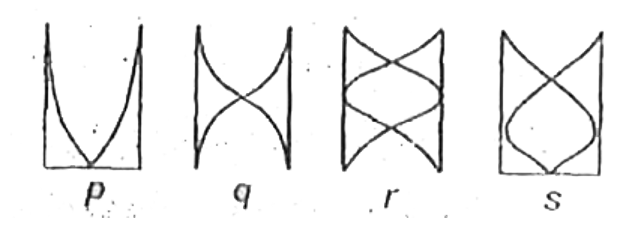Figures shows the vibrations of foue air columns. The ratio of frequencies $n_{p} : n_{q} : n_{r} : n_{s}$ is

A

12:3:3:4

B

1:2:4:3

C

4:2:3:1

D

4:3:2:1

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

|

Answer

Step by step video, text & image solution for Figures shows the vibrations of foue air columns. The ratio of frequencies n_(p):n_(q):n_(r):n_(s) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS SOUND WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The vibrations of four air columns are represented in the adjoining figures. The ratio of frequencies $n_{p} : n_{q} : n_{r} : n_{s}$ is

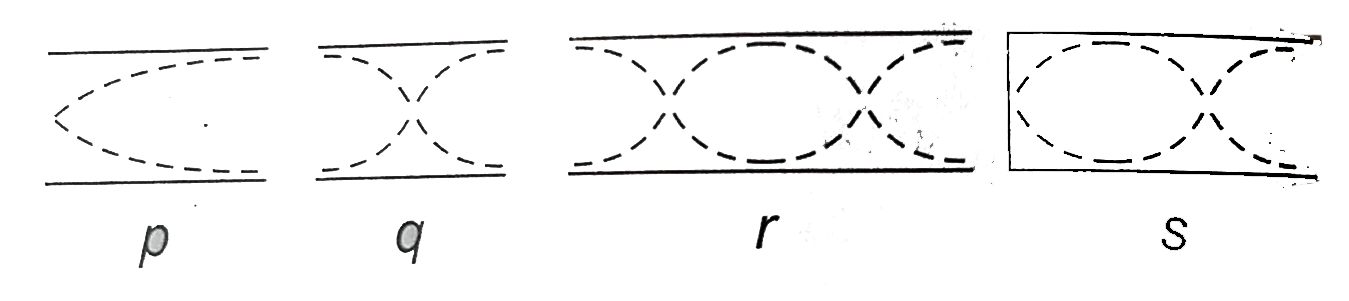A $12 : 6 : 3 : 4$
B $4 : 2 : 3 : 1$
C $1 : 2 : 4 : 3$
D $1 : 2 : 3 : 4$
Question 2 - Select One
A sonometer wire when vibrated in full length has frequency n. Now, it is divided by the help of bridges into a number of segments of lenths $l_{1}, l_{2}, l_{3} \dots$ when vibration these segments have frequencies $n_{1}, n_{2}, n_{3},,,$ Then, the correct relation is
A $n = n_{1} + n_{2} + n_{3} + ... ... ... .$
B $n^{2} = n_{1}^{2} + n_{2}^{2} + n_{3}^{2} + ... ... ... .$
C $\frac{1}{n} = \frac{1}{n_{1}} + \frac{1}{n_{2}} + \frac{1}{n_{3}} + ... ... ... .$
D $\frac{1}{\sqrt{n}} = \frac{1}{{\sqrt{n}}_{1}} + \frac{1}{{\sqrt{n}}_{2}} + \frac{1}{{\sqrt{n}}_{3}} + ... ... ... .$
Question 3 - Select One
The frequency of vibration of air column in a pipe closed at one end is $n_{1}$ and that of the one closed at both end is $n_{2}$ . When both the pipes are joined to form a pipe closed atone end, the frequency of vibration of air column in it is (neglecting end correction )
A $\frac{n_{1} n_{2}}{2 n_{2} + n_{1}}$
B $\frac{2 n_{1} - n_{2}}{n_{1} + n_{2}}$
C $\frac{n_{1} n_{2}}{2 n_{1} + n_{2}}$
D $\frac{n_{1} + n_{2}}{n_{n} - n_{2}}$

BITSAT GUIDE-SOUND WAVES-BITSAT Archives

Home
Ask Doubt
Profile