Which of the following statement(s) is/are true
ionisation energy ∝1Screening effect
The first ionisation energies of Be and Mg are more than ionisation energies of B and Al respectively
Atomic and ionic radii of Niobium and Tantalum are almost same
Metallic and covalent radii of potassium are 2.3A∘ and 2.03A∘ respectively .
The correct Answer is:A, B, C, D
Step by step video, text & image solution for Which of the following statement(s) is/are true by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following statements(s) is/are true for XeF6?
Aits partial hydrolysis gives XeOH4Bits reaction with silica gives XeOF4Cit can be prepared by the reaction of XeF4 and O2F2Dits reaction with XeO3 gives XeOH4Which of the following statements (s)is/are true?
Aa) Differentiable function satisfying f(−1)=f(1) and f'(x)≥0 for all x must be a constant function on the interval [−1,1].Bb) There exists a function with domain R satisfying f(x) lt 0, for all x, f'(x) gt 0 for all x and f''(x0 gt 0 for all x.Cc) If f''(x) = 0 then (c,f(c)) is an inflection point.Dd) Suppose f(x) is a function whose derivative is the function f(x)=2x2+2x−12. Then f(x) is decreasing for −3<x<2 and concave up for x>−12.Which of the following statements (s) is/are true ?
Aa) Differentiable function satisfying f(−1)=f(1) and f'(x)≥0 for all x must be a constant function on the interval [−1,1].Bb) There exists a function with domain R satisfying f(x) lt 0, for all x, f'(x) gt 0 for all x and f''(x0 gt 0 for all x.Cc) If f''(x) = 0 then (c,f(c)) is an inflection point.Dd) Suppose f(x) is a function whose derivative is the function f(x)=2x2+2x−12. Then f(x) is decreasing for −3<x<2 and concave up for x>−12.
Which of the following statements(s) is /are true for XeF6 ?
View SolutionWhich of the following statement(s) is/are with true ?
View SolutionWhich of the following statement(s) is/are with true ?
View SolutionWhich of the following statement(s) is/are with true ?
View SolutionWhich of the following statement(s) are true about Z us P graph for a real gas at a given temperature.
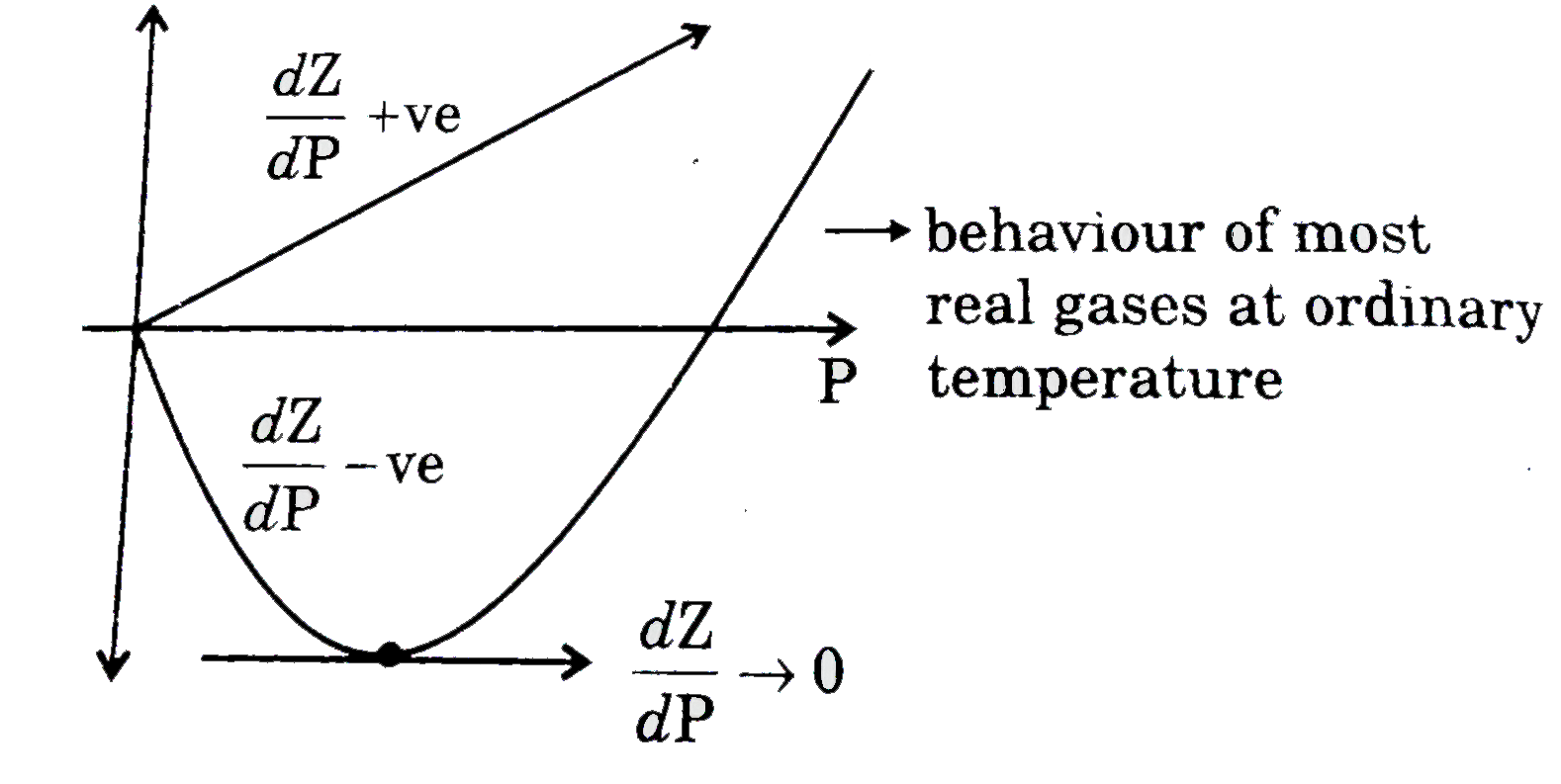
View Solution