Consider a tetrahedron with faces f1,f2,f3,f4. Let →a1,→a2,→a3,→a4 be the vectors whose magnitudes arerespectively equal to the areas of f1,f2,f3,f4 and whose directions are perpendicular to these faces in theoutward direction. Then
Step by step video & image solution for Consider a tetrahedron with faces f_1, f_2, f_3, f_4. Let vec a_1, vec a_2, vec a_3, vec a_4 be the vectors whose magnitudes arerespectively equal to the areas of f_1,f_2,f_3,f_4 and whose directions are perpendicular to these faces in theoutward direction. Then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Consider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
View SolutionLet A be the set of 4-digit numbers a1a2a3a4 where a1>a2>a3>a4, then n(A) is equal to
View Solution
Knowledge Check
Consider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
A1B4C0DNone of theseConsider a tetrahedron with faces F1,F2,F3,F4. Let →V1,→V2,→V3,→V4 be the vectors whose magnitude are respectively equal to areas of F1.F2.F3.F4 and whose directions are perpendicular to their faces in outward direction. Then ∣∣→V1+→V2+→V3+→V4∣∣, equals:
A1B4C0DNone of theseConsider a vector →F=4ˆi−3ˆj. Another vector that is perpendicular to →F is
A4ˆi+3ˆjB6ˆiC7ˆkD3ˆi−4ˆj
Let A be the set of 4-digit numbers a1a2a3a4 where a1>a2>a3>a4, then n(A) is equal to
View SolutionIn a four-dimensional space where unit vectors along the axes are ˆi,ˆj,ˆk and ˆl, and →a1,→a2,→a3,→a4 are four non-zero vectors such that no vector can be expressed as a linear combination of others and (λ−1)(→a1−→a2)+μ(→a2+→a3)+γ(→a3+→a4−2→a2)+→a3+δ→a4=0, then
View SolutionIn a four-dimensional space where unit vectors along the axes are ˆi,ˆj,ˆkandˆl,and→a1,→a2,→a3,→a4 are four non-zero vectors such that no vector can be expressed as a linear combination of others and (λ−1)(→a1−→a2)+μ(→a2+→a3)+γ(→a3+→a4−2→a2)+→a3+δ→a4=0, then a. λ=1 b. μ=−2/3 c. γ=2/3 d. δ=1/3
View SolutionThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
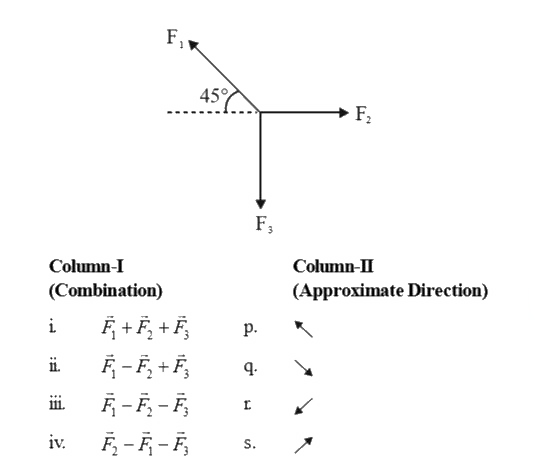
Now match the given columns and select the correct option from the codes given below.
View SolutionThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.

Now match the given columns and select the correct option from the codes given below.
View Solution
