A ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
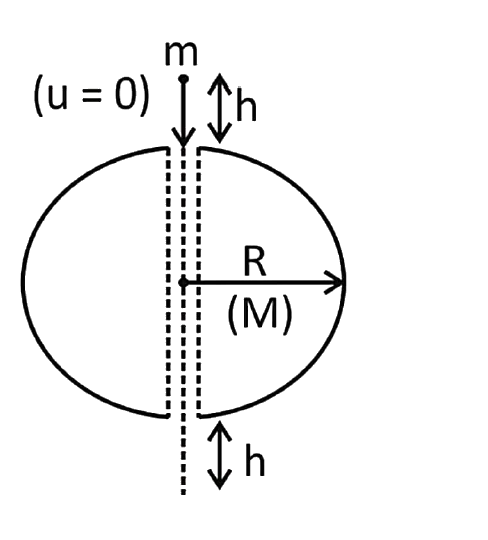
2π√Rg+√2hg
2π√Rg+2√hg
2π√Rg+4√2hg
2π√2Rg+2√hg
The correct Answer is:C
Step by step video & image solution for A ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h < < R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A ball of mass 1 kg is dropped from a height of 5 m. What is its speed at this instant ?
View SolutionAssume that a tunnel is dug across the earth (radius=R) passing through its centre. Find the time a particle takes to cover the length of the tunnel if (a) it is projected into the tunnel with a speed of √(gR) (b) it is relased from a height R above the tunnel (c ) it is thrown vertically upward along the length of tunnel with a speed of √gR.
View Solution
Knowledge Check
A ball of mass m is dropped from a height h equal to the radius of the earth above the tunnel dug through the earth as shows in the figure. Choose the correct options. (Mass of earth =M)
 AParticle will oscillate through the earth to a height h on both sidesBParticle will execute simple harmonic motionCMotion of the particle is periodicDParticle passes the centre of earth with a sped υ=√2GMR
AParticle will oscillate through the earth to a height h on both sidesBParticle will execute simple harmonic motionCMotion of the particle is periodicDParticle passes the centre of earth with a sped υ=√2GMRA particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
AThe motion of the particle is simple harmonicBThe motion of the particle is periodicCThe speed of the particle at the centre of earth equals √2GM(R+h) , where R and M are the radius and mass of the earth respectivelyDThe speed of the particle at the centre of earth equals √GM(R+3h)R(R+h), where R and M are the radius and mass of the earth respectivelyA ball of mass m is dropped from a cliff of height H. The ratio of its kinetic energy to the potential energy when it is fallen through a height 3/4 H is
A3:4B4:3C1:3D3:1
A ball of mass m is dropped from a height of 20 m . The ball loses 20 per cent of its kinectic energy in striking the ground . What will be the height to which the ball will bounce ? Where does this lost energy go ?
View SolutionA block of mass m is dropped from height h above the ground. Find out the speed of the block when it reaches the ground.
View SolutionA satellite of mass m is orbiting the earth at a height h from its surface. If M is the mass of the earth and R its radius, the kinetic energy of the stellite will be
View SolutionA body of mass m is kept at a small height h above the ground. If the radius of the earth is R and its mass is M, the potential energy of the body and earth system (with h=∞ being the reference position) is
View SolutionA satellite of mass m is orbiting around the earth at a height h above the surface of the earth. Mass of the earth is M and its radius is R. The angular momentum of the satellite is independent of
View Solution
