Let f(x)=4x3+1. If the area of the region bounded by f(x) and x-axis from x = 0 to x = a is same as the area of region bounded by f(x) and x-axis from x = a to x = 3 then a lies in (a > 0)
A
(0,1)
B
(1,32)
C
(32,2)
D
(2,3)
Text Solution
The correct Answer is:D

∫aOf(x)dx=∫3af(x)dx
⇒a4+a=84−(a4+a)
a4+a−42=0
Let g(a)=a4+a−42
g(0)<0,g(1)<0,g(3)>0
By IVT
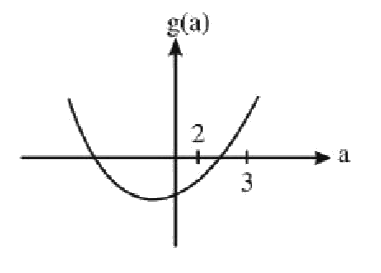
a∈(2,3).
|
Similar Questions
Knowledge Check
The area of the region bounded by the curve y=xsinx, x-axis, x=0 and x=2π is :
A2π sq. unitsB3π sq. unitsC4π sq. unitsD5π sq. unitsThe area of the region bounded by y2=4x,x=0,x=4 and the X-axis in the first quadrant is
A16B163C32D323The area of the region bounded by the curve y=|x−2|,x=1,x=3 and the X-axis is
A1B2C3D4
" Area of the region bounded by "y=x*|x|.2x*1=0" and "x" -axis is "
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View SolutionFind the area of the region bounded by y2=4x,x=1,x=4 and the x-axis in the first quadrant.
View SolutionThe area of the region bounded by the curve y=2x+3 ,x-axis and the lines x=0 and x=2 is
View SolutionThe area of the region bounded by the parabola y=4x−x2, the X-axis, x=0 and x=2 is
View Solution
